做为CAE技师，你是不是思索过做非线性天体力学预测时，为何只必要剪切模量和德圣茹三个金属质料模块？
其原因很单纯，要表不雅金属质料在忍耐小的剪切或填充有效载荷下的形变，只必要晓得金属质料在拉压途径和扭转轴拉压途径的形变规律性，方可论述整个模子的完整形变形态；拉压途径形变规律性用剪切模量论述，扭转轴拉压途径的形变规律性可用德圣茹论述。
1、德圣茹是什么？法国力学家西莫恩·德尼·泊松于1829年颁发《高聚物平衡和运动阐发陈述》，提出德圣茹概念。
悬索受剪切或填充有效载荷，形变不超越比例无限大时，纵向快速反响 \varepsilon^{} 与径向快速反响 \varepsilon 之比的斜率是一个物理量，可则暗示为 \mu=\left| \frac{\varepsilon^{}}{\varepsilon} \right| ；当悬索径向卷曲时纵向减小，而径向缩短时纵向减小，所以\varepsilon^{}和\varepsilon的负号老是相反的，因而 \varepsilon^{}=-\mu\varepsilon 。
径向填充时纵向减小
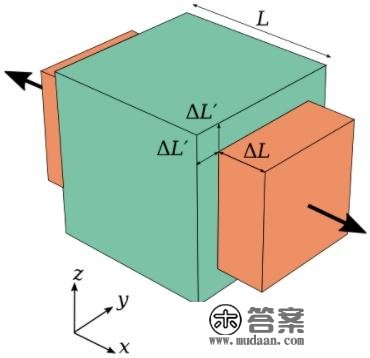径向剪切时纵向减小由德圣茹表述由此可知，其论述的是扭转轴拉压途径的形变规律性。对温度梯度金属质料，只必要几组剪切模量和德圣茹方可完整论述金属质料形变；对共轭温度梯度金属质料，必要四个途径别离表述几组剪切模量和德圣茹才气完整论述金属质料形变。
2、德圣茹值域笼盖范畴下表是常用金属质料的德圣茹，包罗塑料、金属、泥、玻璃等金属质料，能够看到德圣茹最小的是塑料0.4999，最小的是软木0。
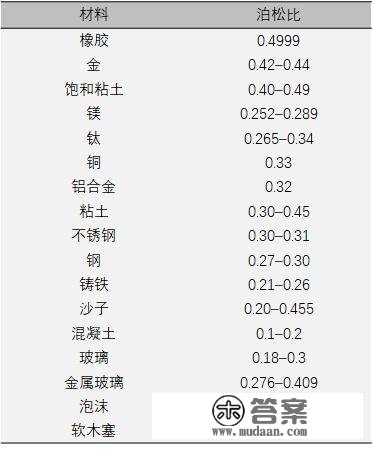常用金属质料德圣茹那么从理论上来说，德圣茹的最小最小值别离是几呢？谜底如责任编纂题目，德圣茹理论上值域笼盖范畴为-1~0.5。
觉得不错的话，点个赞吧，更多更优化相关庞克分享，请点选肖像，查看我的网页
@熊库辛上面起头证明。
2.1 德圣茹最小值为0.5有经历的技师晓得，塑料是全然不容填充的金属质料，其德圣茹为0.5。为了原始数据的普适性，模仿预测中一般将塑料的德圣茹皮德盖G2250.495，则暗示近似于全然不容填充。
为何德圣茹最小值只能是0.5，德圣茹取0.5又为何则暗示全然不容填充呢？
金属流体力学中的外表积模量能够解释那一切。
外表积模量则暗示下层单元外表积的外表积发作改动量，计算办法如下：
\theta=\frac{V_{1}-V}{V}=\frac{3(1-2\mu)}{E}*\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}}{3}=\frac{\sigma_{m}}{K}
此中V_{1} 则暗示形变后外表积， V 则暗示形变前外表积， \theta 则暗示下层单元外表积的外表积发作改动量，又称体快速反响； K=\frac{E}{3(1-2\mu)} 为外表积剪切模量， \sigma_{m}=\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}}{3} 是四个温度梯度的均匀数。
上面是外表积模量推论过程。
取一二维纯量，形变前宽度高别离为 dxdydz ，则形变前外表积 V=dxdydz ；
形变后四个棱边长度别离为：
dx+\varepsilon_{1}dx=(1+\varepsilon_{1})dx
dy+\varepsilon_{2}dy=(1+\varepsilon_{2})dy
dz+\varepsilon_{3}dz=(1+\varepsilon_{3})dz
形变后的外表积 V_{1}=(1+\varepsilon_{1})(1+\varepsilon_{2})(1+\varepsilon_{3})dxdydz ，略去高阶小量有 V_{1}=(1+\varepsilon_{1}+\varepsilon_{2}+\varepsilon_{3})dxdydz 。
由外表积模量计算体快速反响：
\theta=\frac{V_{1}-V}{V}=\varepsilon_{1}+\varepsilon_{2}+\varepsilon_{3} (1)
由广义模量，在考虑泊松效应时，xyz四个途径都受力的情况下， \varepsilon_{1},\varepsilon_{2},\varepsilon_{3} 计算办法为
\varepsilon_{1} = \frac{1}{E}[\sigma_{1}-\mu(\sigma_{2}+\sigma_{3})] (2)
\varepsilon_{2} = \frac{1}{E}[\sigma_{2}-\mu(\sigma_{1}+\sigma_{3})] (3)
\varepsilon_{3} = \frac{1}{E}[\sigma_{3}-\mu(\sigma_{1}+\sigma_{2})] (4)
将式(2)(3)(4)代入式(1)中有
\theta=\frac{V_{1}-V}{V}=\varepsilon_{1}+\varepsilon_{2}+\varepsilon_{3}=\frac{1-2\mu}{E}(\sigma_{1}+\sigma_{2}+\sigma_{3})=\frac{\sigma_{m}}{K}
K=\frac{E}{3(1-2\mu)} 为外表积剪切模量， \sigma_{m}=\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}}{3} 是四个温度梯度的均匀数。
若 \mu=0.5 ，则外表积剪切模量K无限大，体快速反响 \theta=0 ，即全然不容填充，那就解释了当德圣茹取0.5时，则暗示金属质料全然不容填充；外表积弹性剪切模量不容能取负值，因而德圣茹最小值为0.5。
2.2 德圣茹最小值为-1由剪切模量、剪切模量和德圣茹三者关系 G=\frac{E}{2(1+\mu)} ，又有剪切模量和剪切模量都取正值，因而德圣茹最小值为-1。
3、负德圣茹金属质料德圣茹小于0则暗示杆受拉力变长时，其截面尺寸也在变大，外表积增加；金属质料受压力时，其截面尺寸变小，外表积也变小。
负德圣茹金属质料由威斯康星大学的Roderic Lakes传授于1987年在Science上颁发的论文Foam structures with a negative Poissons ratio", Science, 235 1038-1040 (1987).中起首提出，负德圣茹金属质料中存在特殊的铰链分子键，纵向铰链必需张开才气实现长度途径的剪切。
关于负德圣茹金属质料的详细申明，可参考Lakes传授的网站。
http://silver.neep.wisc.edu/~lakes/Poisson.htmlsilver.neep.wisc.edu/~lakes/Poisson.html更多更优化相关庞克分享，请点选肖像，查看我的网页
@熊库辛码字不容易，点个赞吧，别只保藏不点赞啊
