数学家用很长时间证明等周问题是在追求什么?
好的,就着那个问题来讲一劣等周问题。
平面上的等周问题长短常古老的问题,在维吉尔的史诗《埃涅阿斯纪》中就呈现了等周问题的影子。等周定理简单归纳综合就是,在平面上给定长度的简单闭曲线中,圆周所围的面积更大。圆那一谜底看似天然而合理,但要严酷地证明却其实不容易,汗青上研究该问题的数学家屡见不鲜,今天我们就开启一趟数学摸索之旅,体味那些差别气概的证明办法。撰文 | 杨帆(重庆DX数学与统计学院)
一出名歌剧里的数学问题
平面上的等周问题是微分几何的根本问题之一,研究汗青悠久,若要完好的讲述此中的故事,我们无妨从亨利·普赛尔(Henry Purcell, 1659-1695)最出名的歌剧《狄朵与埃涅阿斯》(Dido and Aeneas)聊起。那部歌剧取材于维吉尔(Virgil)的史诗《埃涅阿斯纪》(Aeneid),演绎了迦太基(Carthagia)女王狄朵和特洛伊英雄埃涅阿斯的恋爱悲剧,歌剧中女巫姐妹为了毁坏他们的恋爱,棍骗埃涅阿斯分开迦太基去完成一项任务,狄朵误认为他变节了本身,于是自焚身故。
最末,他们呈现在你面前,
能够看到新迦太基建起的塔楼;
在那里买下一块地盘,名叫比尔萨。
——《埃涅阿斯纪》
歌剧《狄朵与埃涅阿斯》宣传图狄朵与埃涅阿斯的相遇其实其实不浪漫,她一生命途坎坷,在此之前因丈夫被谋害而被迫逃离故乡,她一路流亡来到北非海岸,并设法在此定居,为购置地盘与本地人履历了一番讨价还价,最末得到的许诺是她只能占有一块牛皮包住的地盘,于是聪明的狄朵将牛皮切成尽可能多的细条,将细条相连成线从而围住了大片地盘。在那里我们看到了等周问题的影子——在给定的周长内围住尽可能多的地盘面积,遗憾的是那位潜在的女数学家选择将生命献给恋爱,最末那个数学问题仍是由古希腊数学家给大致处理了。
何为等周定理?即平面上定长的简单闭曲线中圆周所围的面积更大,其对偶定理与之等价,即平面上面积相等的几何图形中圆的周长最小。设D是长度为L的平面简单闭曲线,由若尔当曲线定理(即在欧式平面上,肆意一条简单闭曲线D可把平面分红两个部门,使得统一部门的肆意两点可用不与D订交的弧相连),曲线D可围成面积为A的有限区域,用不等式暗示为
,当且仅当D为圆周时等号成立。
等周问题的肥皂泡尝试
谜底看似有理,究竟结果圆是一个如斯奇异的外形,但严酷地证明其实不容易,汗青上先后有许大都学家都研究过该问题,但曲到19世纪,才由德国数学家魏尔斯特拉斯(Weierstrass,1815-1897)初次给出了一个严谨的数学证明(拜见参考文献4)。接下来,我们就来领会几个差别期间有代表性的证明办法。
二 斯坦纳的证明
在正式证明之前,我们要明白等周定理的解必然是凸几何。所谓凸几何,即在某一图形内取肆意两点连成线段,若线段上所有的点都在图形内,则该图形为凸几何,反之为非凸几何。
假设曲线D围成了一个面积更大的图形(如下图所示),用一条曲线平分曲线D的周长,如许就得到了两段等长的曲线D1与D2;之后将D1与D2别离关于曲线做对称,围成新图形A1、A2,此时A1与A2的周长与面积均相等。诶,等等,你确定面积也必然被平分吗?当然啦!若是平分周长时面积并未被平分,那么将原图形中面积更大的一半关于曲线做对称,就能得到周长相等而总面积更大的图形,从而与假设矛盾。
等周问题的解必然是凸几何
无妨假设A1为非凸几何,能够做一条与曲线凹处订交的曲线,从而得到两个交点A与B,此时线段AB中存在A1以外的点,将两交点间的曲线段关于交线做对称,如许A1的周长稳定,而面积却增大了,那意味着曲线D能够围成面积更大的图形,与假设矛盾。因而,简单闭凸曲线方可围成面积更大的图形,明白那一点能够大大简化证明的过程。
17世纪以来,一批数学家们努力于在处理几何问题时尽量少的运用代数运算,而逃求更具普适性的办法,雅各布·斯坦纳(Jakob Steiner,1769-1863)就是此中一位代表性人物。他在合成几何方面的研究较为权势巨子,他认为计算阻碍了思虑,而地道的几何学则刺激了缔造性思维,在他所给出的五种对等周定理的证明中,那一立场也有所表现,我们先来领略此中两种办法的出色之处。
Jakob Steiner,1769-186301
四铰链证明法
(Four-hinge Proof)
与之前的做法类似,起首用一条曲线将定长前提下面积更大的图形分为周长相等的两部门,此时面积也被平分,要证明等周定理,只要证明图形平分后的两部门为半圆。
考虑上半部门曲线 D1 围成的图形A1,运用反证法,假设A1不是半圆。将D1与朋分线的交点记为B与C,由曲角三角形的斜边中线定理可知,半圆的内接三角形为曲角三角形,而A1不是半圆,则D1上存在一点A,与点B、C相连使得∠A不是曲角。接着,挪动三角形底边的端点 B、C,并连结BA、CA的长度稳定,使∠A变成曲角,那时,连结暗影部门面积稳定,而三角形△ABC面积增加,从而A1的面积也增加,而曲线 D1 的长度未变,因而在周长稳定的情况下得到了面积更大的图形,与假设矛盾,因而上半部门为半圆,从而圆就是面积更大的图形。
02
均匀鸿沟证明法
(Mean-boundray Proof)
起首来介绍一下均匀鸿沟的概念,能够将它理解为两条给定曲线的中线,从垂曲标的目的看,做不断线与三条曲线别离交于A、B、C,则线段AB与线段BC等长。而且稍做计算能够发现,均匀鸿沟的长度不大于两条给定曲线长度的均匀值,只要当两条曲线一样时才气取等号。
均匀鸿沟
与前一种证法类似,假设曲线D所围图形面积更大,将其按周长平分为曲线D1、D2(如下图所示),无妨将曲线D2关于朋分线做对称,使两段曲线处于统一侧,D1 与 D2 所围区域别离为A1、A2。接着做出它们的均匀鸿沟,此时,均匀鸿沟所围的面积能够暗示为
此中,S(·) 暗示面积,
暗示两段曲线所围的堆叠区域,因而均匀鸿沟所围面积为原面积的一半。但曲线D1、D2其实不能对称重合,所以均匀鸿沟的长度小于周长的一半,根据等周定理的对偶定理,显然矛盾。因而原图形平分后的两段曲线必需在对称后重合,从而曲线所围成面积更大的图形是圆。
斯坦纳等一寡数学家的勤奋让群众相信,离开了代数与阐发的数学仍旧是强大的兵器,但我们同时又会如斯逼真地感触感染到几何与方程碰碰产生的奇奥成果。因为下文会用到面积公式,无妨先用几何的办法来推导一下。
三角形的面积谁城S算,但换一种思绪,运用几何曲不雅即可得到另一种表达体例。起首引入三角形的外接矩形,之后根据填补色块的思绪简单推导就得到的另一种形式的面积公式。若将三角形顶点置于平面坐标系的第一象限中,逆时针标的目的付与顶点坐标,则三角形面积为 A=(x1y2-x2y1)/2。
对多边形能够停止类似的推广,若将n边形置于第一象限,以逆时针标的目的看各顶点坐标为 (0, 0),(x1, y1), ..., (xn-1, yn-1),则该 n 边形的面积为
将其转化为积分的形式就是:
常常提到计算平面图形的面积,总会前提反射似的想到格林公式(Green Formula,即
),而几何的体例又给我们供给了另一种理解体例。值得一提的是,斯坦纳的证明皆是基于解的存在性假设,那一点使他的证明其实不严谨,以至有同业用歌剧中狄朵的最初一句话来调侃他:“铭刻我,但啊,忘了我的命运吧。”(Remember me, but ah! Forget my fate.)如斯看来,几何办法还需要与其他数学常识相连系才气更好地阐扬其效用,因而在十九世纪与其他数学学派的合作中,以斯坦纳为首的对峙纯几何办法的学派明显处于了优势。
三后斯坦纳时代
尔后,存在性的问题不断无人能解,曲到1879年魏尔斯特拉斯在一次讲座中证了然解的存在性,从而使等周问题拥有了第一个严谨的证明。完好地证明解的存在性长短常困难的,连魏尔斯特拉斯本身都慨叹:“那个问题其实是太难了,以致于它被认为几乎不克不及被完成。”因而本文对此就不停止深切的介绍了。
在证了然解的存在性的后斯坦纳时代,数学家们对等周问题的研究似乎多了些底气,下面介绍了两种差别的证明办法,我们无妨体味一下差别气概的证明之美。
01
变分法证明
Jakob Bernoulli (1654-1705) 和 Johann Bernoulli (1667-1748)
变分法更先由约翰·伯努利(Johann Bernoulli)于1696年提出,起初是为领会决物理中的最速降线问题,雅克布·伯努利(Jakob Bernoulli)晓得后也起头潜心研究,那个问题同时也吸引了欧拉、牛顿等数学家的留意,在一幕数学家的通力合作下,变分法的研究不竭获得打破。值得一提的是那伯努利两兄弟的关系,哥哥雅各布一生渐渐五十载,而此中的三十年都用在了和弟弟停止学术争论上,在我们后人看来,恰是他们对科学不竭的切磋争论,才促进了科学的开展与前进。
等周问题十分简洁,所给的前提只要定长那一个,若把面积更大理解为求极值,那么用变分法处置就显得十分天然。变分法的核心思惟是找到一个函数y(t),求得与之相关的泛函
的极值。
在处理等周问题时,我们就需要找到曲线t→(x(t), y(t)),在给定周长
的前提下,使面积
更大化,运用拉格朗日乘子法(Lagrange Multiplier Method)构造函数:
并求出
的极值。
变分法的关键是欧拉方程(Euler Equation),即通过使一阶导为零求得极值点,别离化简 x 与 x’ 的欧拉方程求得最末解,那显然是圆参数方程的一种形式。
02
投影法证明
施密特( Erhard Schmidt)的投影法证明办法的奇特之处在于,运用投影的办法将不规则图形与圆周相联络,详细做法是将简单闭曲线α所围成的区域夹在两平行曲线之间,在两曲线间做一半径为r的圆周β,以圆心为原点,y轴与曲线平行成立平面曲角坐标系,令
,
,如许就能够计算它们各自的面积。此中,s为曲线α的弧长参数,A为曲线α围成的面积。
将原曲线投影到圆周上
将两者面积相加,运用柯西不等式停止放缩,在计算过程中需要留意一个隐含前提,因为对原曲线做了弧长参数化处置,则有弧长参数x2+y2=1,计算时可停止化简,最末求得等周不等式,当等号成立时 A= πr2,L=2πr,因而原曲线围成的就是一个圆。
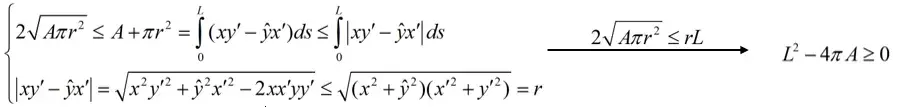
说了那么多,等周定理到底有什么用呢?操纵最短的线围出更大的面积是其在日常生活中最为常见的应用。等周定理不像莫比乌斯环、哥尼斯堡七桥问题、四色问题等那么为人熟知,但它在鞭策学术研究上具有重要价值,例如该定理可用来停止特征值估量,处理流体机械中的流化感化相关的问题等。感兴趣的小伙伴能够停止更深切的研究。(拜见《2018年菲尔兹奖得主:在天然里寻找不变性的游览者》)
回忆等周定理的各类证明,数学家和文学家的思维一样灵敏而自在,同样的事物在他们眼中会酿成差别的光景,差别的办法让我们能够从差别的角度去理解统一个事实,那往往引导出数学上差别的开展。
王国维在《人世词话》中将词分为有我之境与无我之境,借用丘成桐先生的概念,数学研究当然也有境界的概念,在某种水平上也可谈有我之境、无我之境。等周问题生发于现实中的买地问题,由生活引导,可谓无我之境;但随后数学家们不懈的证明鞭策理论的开展,可谓有我之境矣。

参考文献
[1] https://math.berkeley.edu/~hutching/pub/bubbles.html.
[2] https://v.电话.com/x/page/j0915p3fxyh.html.
[3] Viktor Blasjo. The Evolution of The Isoperimetric Problem. The Mathematical Association of America. 2005.
[4] K. Weierstrass. Mathematische Werke. Mayer and Muller. Berlin. Vol.7. 1927.
[5] 沈一兵. 整体微分几何初步. 高档教育出书社. 2009.
版权声明
本文仅代表作者观点,不代表木答案立场。
