吐血整理!2020高考数学评分细则参考,2021这样准备少丢分!
高考大题承袭按步调做答、按步调给分的原则,哪些步调是有分可拿的?哪些步调是能够S略的?若是标题问题不会做,若何通过步调多得几分?一切尽在评分细则!
固然高考命题组不会发布昔时的评分细则,但各DX校的名师每年城S根据阅卷经历,推表演昔时的评分细则参考,学魁君给各人整理出了2020年高考数学的评分细则,2021考生能够参考!
 2020高考数学评分细则参考
2020高考数学评分细则参考
1.数学阅卷流程
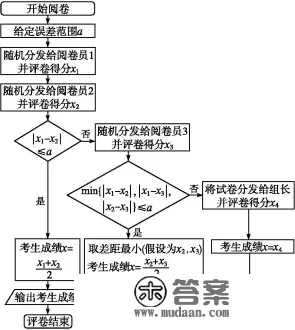
 2.分题型展现
2.分题型展现
题型一 三角形解答题
高考实题:

(一)评分尺度展现——看细节

(二)一题多解鉴赏——扩思绪
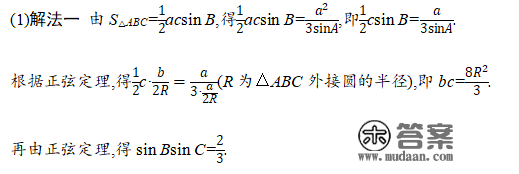

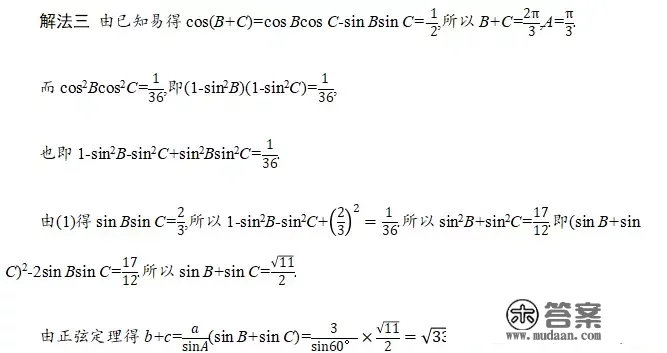
(三)阅卷教师提醒——明原因
三角函数标题问题属于高考题中的低中档题,但每年考生的得分情况都不睬想,如公式记忆不清、解题办法不明、解题办法选择不妥等问题屡屡呈现,不克不及包管做答“会而对,对而全,全而美”。下面就以2017年高考数学全国卷Ⅰ理科第17题为例停止阐发申明。
1.常识性错误

2.战略性错误

(四)新题好题练习训练——成习惯

题型二 数列解答题
(2016全国,文17)(本小题满分12分)已知{an}是公役为3的等差数列,数列{bn}满足b1=1,b2=,anbn+1+bn+1=nbn.(1)求{an}的通项公式;(2)求{bn}的前n项和。
(一)评分尺度展现——看细节

(二)一题多解鉴赏——扩思绪
解法二

(三)阅卷教师提醒——明原因

(四)新题好题练习训练——成习惯

题型三 概率与统计解答题
(2017全国2,文19)(本小题满分12分)海水养殖场停止某水产物的新、旧网箱养殖办法的产量比照,收成时各随机抽取了100个网箱,丈量各箱水产物的产量(单元:kg),其频次散布曲方图如下:
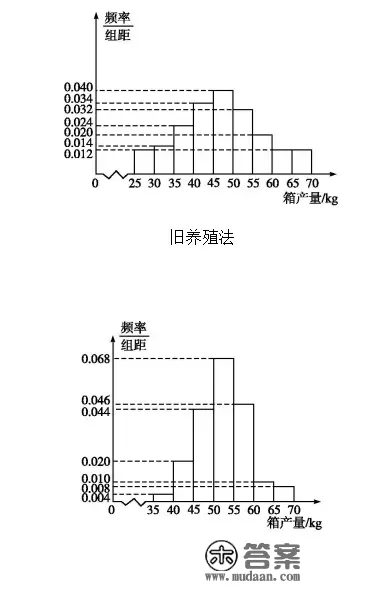
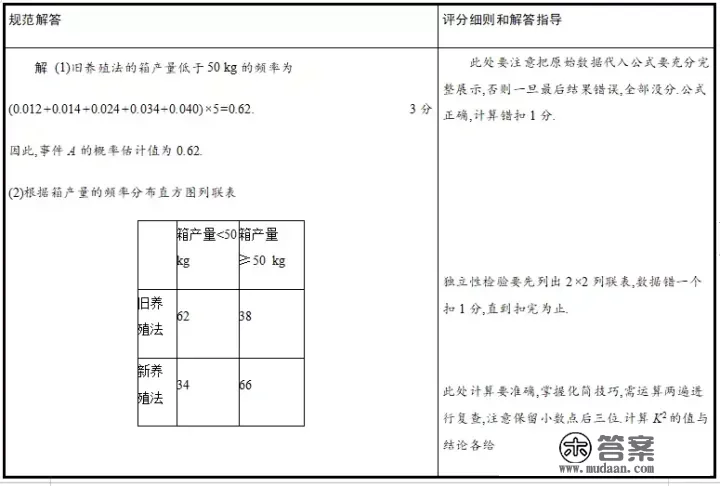
(1)记A暗示事务“旧养殖法的箱产量低于50 kg”,估量A的概率;
(2)填写下面列联表,并按照列联表判断能否有99%的掌握认为箱产量与养殖办法有关;

(3)按照箱产量的频次散布曲方图,对那两种养殖办法的好坏停止比力.

(一)评分尺度展现——看细节

(二)阅卷教师提醒——明原因
1.准确阅读理解,弄清题意:与概率统计有关的应用问题经常以现实生活为布景,且常考常新,而处理问题的关键是理解题意,弄清素质,将现实问题转化为数学问题求解。
2.对互斥事务要掌握住不克不及同时发作,而关于对立事务除不克不及同时发作外,其并事务应为一定事务,那些也可类比集合停止理解,详细应用时,可把所有试验成果写出来,看所求事务包罗哪几个试验成果,从而判定所给事务的关系。
3.用频次散布曲方图处理相关问题时,应准确理解图表中各个量的意义,识图掌握信息是处理该类问题的关键。
4.某些数据的变更对中位数可能没有影响。中位数可能呈现在所给数据中,也可能不在所给数据中。当一组数据中的个别数据变更较大时,可用中位数描述其集中趋向。均匀数与方差都是重要的数字特征,是对总体的一种简明的描述,它们所反映的情况有着重要的现实意义,均匀数、中位数、寡数描述其集中趋向,方差和尺度差描述其颠簸大小。
5.独立性查验的留意事项(1)在列联表中留意事务的对应及相关值确实定,不成混淆。K2的不雅测值k的计算公式很复杂,在解题中易混淆一些数据的意义,代入公式时出错,而招致整个计算成果出错。(2)对判断成果停止描述时,留意对象的拔取要准确无误,应是对假设结论停止的含概率的判断,而非其他。
(三)新题好题练习训练——成习惯
(2018四川凉山诊断性检测)为领会男性家长和女性家长对gz学生成人礼节式的承受水平,某ZX团委以问卷形式查询拜访了50位家长,得到如下统计表:
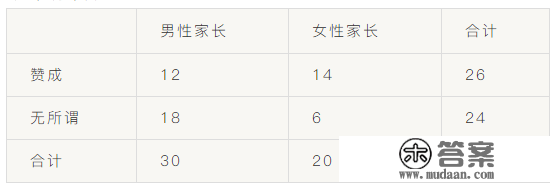
(1)据此样本,能否有99%的掌握认为“承受水平”与家长性别有关?申明理由;
(2)XX决定从男性家长中按分层抽样办法选出5人参与本年的gz学生成人礼节式,并从中选2人交换发言,求发言人中至多一人持“赞成”立场的概率。
参考数据
P(K2≥k)0.050.010k3.8416.635


题型四 立体几何解答题
(2017全国3,文19)(本小题满分12分)如图,四面体ABCD中,△ABC是正三角形,AD=CD。
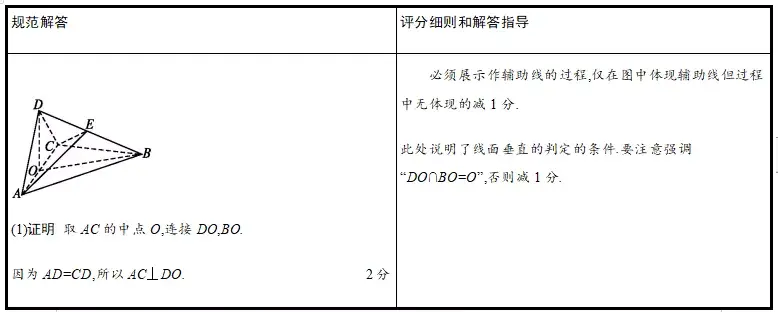
(1)证明:AC⊥BD;
(2)已知△ACD是曲角三角形,AB=BD。若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比。

(一)评分尺度展现——看细节
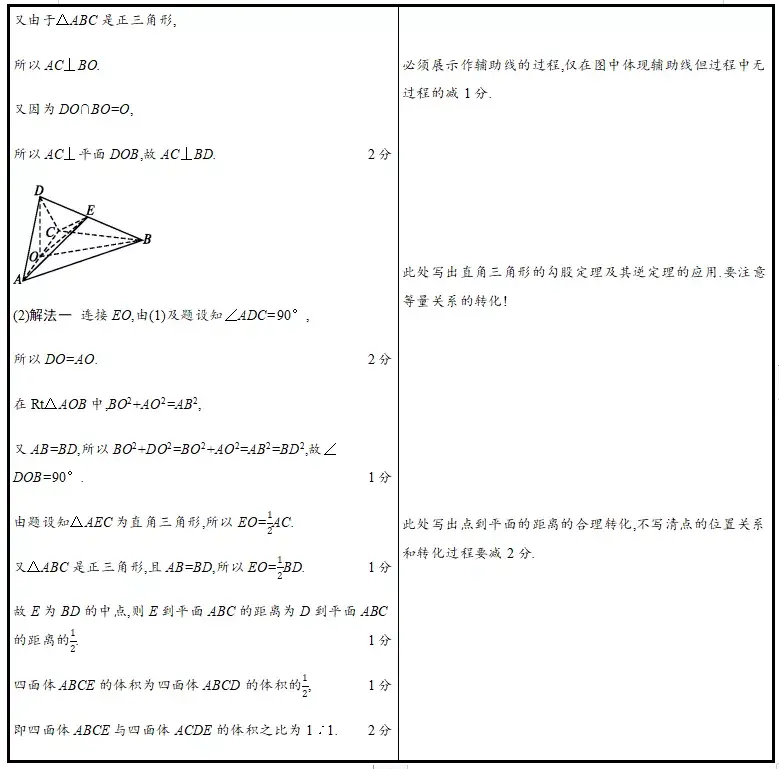
(二)一题多解鉴赏——扩思绪

(三)阅卷教师提醒——明原因
1.证明线面垂曲时,不要轻忽“面内两条曲线为订交曲线”那一前提,如第(1)问中,学生易轻忽“DO∩BO=O”,招致前提不全而减分;
2.求四面体的体积时,要留意“等体积法”的应用,即合理转化四面体的顶点和底面,目标是底面积和顶点到底面的间隔容易求得;
3.留意操纵第(1)问的成果:在题设前提下,若是第(1)问的成果第(2)问能用得上,能够间接用,有些标题问题不消第(1)问的成果以至无法处理,如本题中,由(1)及题设知∠ADC=90°。
4.要留意书写过程标准,计算成果准确。书写标准是计算准确的前提,在高考那一特定的情况下,学生更要连结标准书写,力争一次胜利,但部门学生因日常平凡习惯,解答过程中书写紊乱,招致失误过多。
(四)新题好题练习训练——成习惯
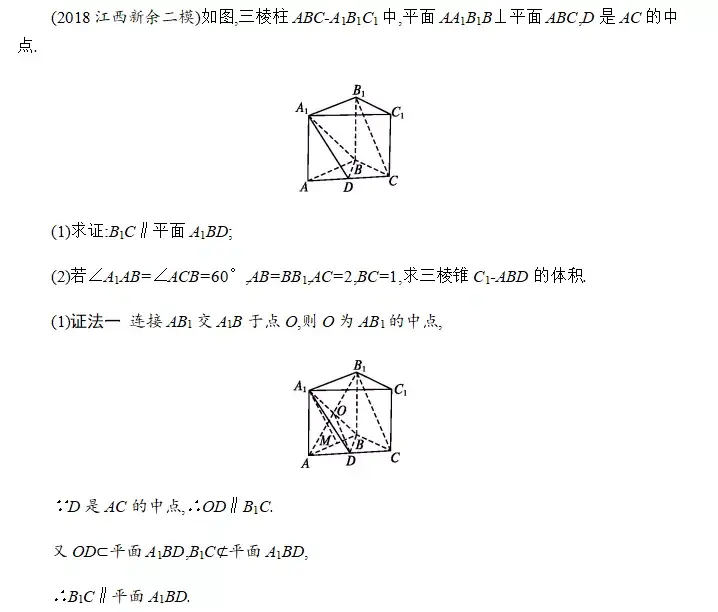




题型五 解析几何解答题

(一)评分尺度展现——看细节

(二)一题多解鉴赏——扩思绪


(三)阅卷教师提醒——明原因

(四)新题好题练习训练——成习惯



题型六 函数与导数解答题
(2017全国2,文21)(本小题满分12分)设函数f(x)=(1-x2)ex.(1)讨论f(x)的单调性;(2)当x≥0时,f(x)≤ax+1,求a的取值范畴.
(一)评分尺度展现——看细节


(二)一题多解鉴赏——扩思绪
解法二设g(x)=(x2-1)ex+ax+1,x≥0,
则g(x)≥0 恒成立.
g(x)=(x2+2x-1)ex+a.
g ″(x)=(x2+4x+1)·e2>0,g(x) 在区间[0, +∞) 内单调递增.
当a≥1 时, g(x)≥g(0)=-1+a>0, 此时g(x) 在区间[0, +∞) 内单调递增, g(x)≥g(x)=0, 契合题意.
当a<1 时, g(0)=-1+a<0,
当x≥1 时, x2+2x-1≥2,
取x1=ln(e+a),
则g(x1)≥2(e+|a|)+a=2e+|a|+(|a|+a)>0,
故存在x0>0, 使得g(x0)=0, 且当x∈(0,x0) 时, g(x)<0, 此时g(x) 单调递加, g(x)<g(0)=0, 不契合题意.
所以, a的取值范畴是[1, +∞).
解法三构造函数g(x)=(1-x2)ex-ax-1, 则g(x)=(-x2-2x+1)ex-a.
因为g(0)=0, 故必然存在x0>0, 使得x∈[0,x0] 时, g(x)≤0.( 若否则, 即肆意x0>0,x∈[0,x0] 时g(x)>0, 则x∈(0,x0),g(x)>0 时, 不契合题意) .从而有g(0)=1-a≤0, 即a≥1.
下面证明a=1 时, g(x)=(1-x2)ex-x-1≤0(x≥0) 恒成立.因为g(x)=(-x2-2x+1)ex-1,g ″(x)=(-x2-4x-1)ex<0, 知g(x) 在[0, +∞) 内单调递加, 且g(0)=0, 故g(x)≤0,[g(x)]max=g(0)=0≤0, 故a的取值范畴是[1, +∞).( 也可间接证明a≥1 时, g(x)=f(x)-ax-1≤0 成立)
(三)阅卷教师提醒——明原因
1.操纵导数研究函数或不等式问题时,准确求导是第一步,也是关键一步,而学生往往起头求导就呈现错误,后面的运算全数酿成了无用功;
2.分类讨论处理问题时,起首要明白分类的根据和尺度;分类讨论思惟是gz数学中的一种重要思惟,也是学生的难点,关键要搞清“为什么要讨论?”“若何去讨论”,如本题中,需要讨论a与0,1的大小关系。
3.要留意书写过程标准,计算成果准确。书写标准是计算准确的前提,在高考那一特定的情况下,学生更要连结标准书写,力争一次胜利,但部门学生因日常平凡习惯,解答过程中书写紊乱,招致失误过多。
(四)新题好题练习训练——成习惯
(2018 河北保定一模) 已知函数f(x)=x+.
1) 判断函数f(x) 的单调性;
(2) 设函数g(x)=ln x+1,证明: 当x∈(0,+∞), 且a>0 时,f(x)>g(x)。
(1)解因为f(x)=1-(x≠0),
①若a≤0,f(x)>0,
∴f(x) 在( -∞,0),(0,+∞) 为增函数;
②若a>0, 则f(x)>0⇒x2-a>0⇒x<-或x>,
f(x)<0⇒x2-a<0⇒-<x<(a≠0),
∴函数f(x) 的单调递增区间为( -∞,-),(,+∞),
单调递加区间为( -,0),(0,);


题型七 参数方程与极坐标解答题

(一)评分尺度展现——看细节

(二)一题多解鉴赏——扩思绪

(三)阅卷教师提醒——明原因
1.根本的定义、公式,办法要掌握安稳:本题第(1)问考察消参求轨迹方程的问题,属于根本问题,第二问求解点在极坐标系下的极径,属于根底概念的考察,但是要求对根本的概念和公式可以纯熟理解和掌握。
2.留意操纵第(1)问的成果:在题设前提下,若是第(1)问的成果第(2)问能用得上,能够间接用,有些标题问题不消第(1)问的成果以至无法处理,如本题便是在第(1)问的根底长进行计算求解极径问题。
3.写全得分关键:写清解题过程的关键点,有则给分,无则没有分,同时解题过程入彀算准确,是得分的底子包管。如本题第(1)问要写出曲角坐标方程,留意所得的轨迹方程不包罗y轴上的点。第(2)问中方程的思惟很重要,联立极坐标方程求解极径、极角表现出方程思惟的无处不在。
(四)新题好题练习训练——成习惯


题型八 不等式选讲解答题
(2017全国3,文23)(本小题满分10分)已知函数f(x)=|x+1|-|x-2|,
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范畴。
(一)评分尺度展现——看细节

(二)一题多解鉴赏——扩思绪

(三)阅卷教师提醒——明原因
1.根本的定义、公式、办法要掌握安稳:本题第(1)问考察绝对值不等式的解法,属于根本问题,第(2)问求解参数的取值范畴,要求同窗们可以连系恒成立的前提停止灵敏变形处置。
2.留意操纵第(1)问的成果:在题设前提下,若是第(1)问的成果第(2)问能用得上,能够间接用,有些标题问题不消第(1)问的成果以至无法处理,如本题便是将原问题转化为求解最值的问题来确定参数的取值范畴。
3.写全得分关键:写清解题过程的关键点,有则给分,无则没有分,同时解题过程入彀算准确,是得分的底子包管。如本题第(1)问要写出分段函数的形式,分段求解不等式的解集。第(2)问直达化的思惟很重要,将原问题转化为求解最值的问题即可,转化的思惟是gz数学的重要数学思惟之一。
(四)新题好题练习训练——成习惯

 3.阅卷根本建议
3.阅卷根本建议
高考数学阅卷对常识点和步调的掌握,公平客不雅,本着给分有理扣分有据的原则,寻找得分点,不然写再多也是徒劳的。但是也并不是完全无情,好比有少数考生答题错位,会被要求做为异常试卷提交,由专家组特殊处置,而不是间接判了零分等。为此,总结如下解题中需要掌握的原则:
1.阅卷速度以秒计,标准答题少丢分
高考阅卷评分尺度十分细,按步调、得分点给分,评阅分步调、采“点”给分。关键步调,有则给分,无则没分。所以考场答题应尽量按得分点、步调标准书写。阅卷中强调存眷成果,过程可接纳差别的办**述。
2.不求巧妙用通法,通性通法要强化
高考评分细则只对次要解题办法,也是最根本的办法,给出详细得分尺度,所以用常规办法往往与参考谜底一致,比力容易抓住得分点。阅卷中掌握见点得分,踩点得分,上下不连累的原则。
3.清洁整洁保得分,简明扼如果关键
若书写整洁,表达清晰,必然会得到合理或偏高的分数,若不标准可能就会吃亏。若写错需矫正,只需划去,不要乱涂乱划,不然易丢分。
4.狠抓根底保成就,分步处理克难题
(1)根底题争获得满分。涉及的定理、公式要准确,数学语言要标准,,认真计算,争取前3个解答题及选考不丢分。
(2)压轴题争取多得分。第(1)问一般难度不大,要包管得分,第(2)问若不会,也要按照前提或第(1)问的结论推出一些结论,可能就是得分点。
综合整理自收集,若有侵权请联络删除!
版权声明
本文仅代表作者观点,不代表木答案立场。
