木答案健康经历过2020最难考研数学后，前辈们给21数学复习提出什么样的建议呢？

经历过2020最难考研数学后，前辈们给21数学复习提出什么样的建议呢？

17小时前 (14:36:19)阅读1回复0

zaibaike

管理员
注册排名1
经验值179065
级别管理员
主题35813
回复0

楼主

本篇约11200字，原创不容易，若有收成请文末来个赞，以鼓舞创做更多优良内容！

2020年数学测验完毕后到如今的7月，各路平台上不断在议论考题的难易。

有人说标题问题几乎难爆了，有人说与往年持平，有人说标题问题新颖没见过，有人灰心地宣扬"实题无用论"……总体来说，认为考题难的声音更多一些。

但，无论若何评价实题的难度，都只是小我的主不雅感触感染，与小我的复习程度有关，不敷客不雅。不克不及因为说难的人多，就受从寡心理影响，本身也跟着认同，从而对考研数学产生畏惧。克制从寡心理，独立客不雅地阐发问题，才是难能宝贵的。

我认为，评测实题难易水平的一个重要客不雅目标是：能否在历年实题中呈现过类似实题。

历年实题，相当于一个对每小我都开放的公共题库，若是在历年实题中呈现的类似题型的数目比力多，就能够断言，实题很有用！

接下来，会以2020年数学一实题为例，先统计类似实题情况并数据可视化，再给出结论，最初，详细给出每一道题的思绪、详细解析、难易度、立异度、类似实题。

为什么要做那项工做？一是给21年考数学的考生一颗定心丸，以至很多考生都被20年实题吓得改了目的专业；二是想告诉各人，你们不断对峙的概念是没错的——实题是最有价值的习题！

一、历年类似实题统计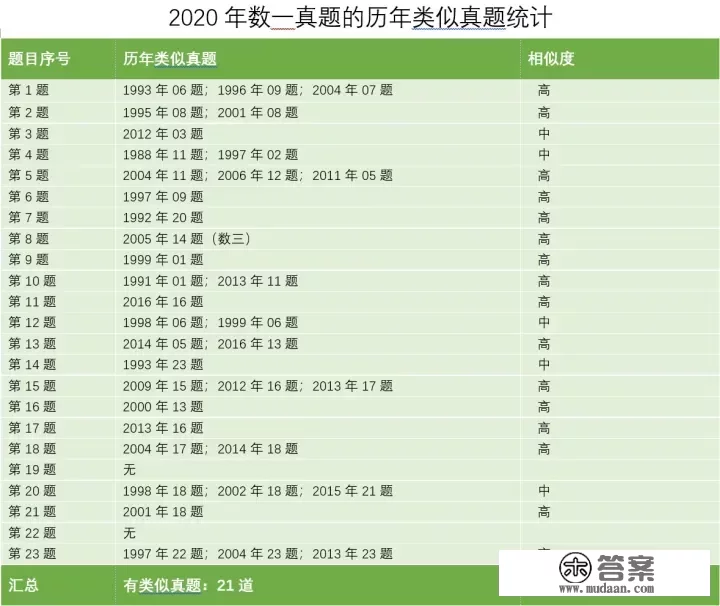

统计以数一实题为主，其他类别为辅，且某些题只列出一部门类似实题

从上述表格可知两点：

一、绝大大都标题问题（21道）都有“原型”；

二、良多比力立异的标题问题与早期（2008年以前）的实题题型十分类似。

本文通篇看完你会发现，当范畴放大到更早年份的实题时，本年的良多貌似新颖的标题问题并非非常地“立异”。

当然，2008年以前纲领不断在做调整，整体难度要比之后的年份略高一点。

那还需要什么考前押题班？实题就是了啊，你想要的都在实题中！有兴趣的同窗能够鄙人文的实题详细解析part比照一下。下面继续来看分值比例。

二、统计成果的饼状图

有类似实题的（高类似度）：16道题，共102分；

有类似实题的（中类似度）：5道题，共27分；

没有类似实题的：2道题，共21分。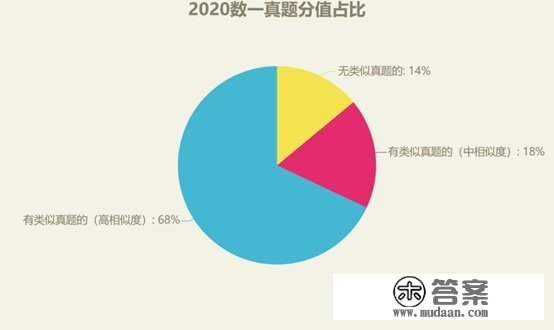

从饼状图能够看出，若是实题做的十分熟练，更高能拿到有高类似度的类似实题的标题问题分数（102分），题型和思绪都是高度类似的，努勤奋，过国度线应不成问题；

若是思维能略微转个弯，能触类旁通的，进一步能拿到有中类似度的类似实题的标题问题分数（27分）；

剩下没有类似实题的标题问题分数（21分），只能靠日常平凡积累的根本功力，详细问题详细阐发了。此中，第19题是高数压轴题，确实难，第一问略难，只要想到用拉格朗日，就有可能推出来，第二问很难，那5分能够放弃。第22题很新颖，但说实话其实不难，思绪与一维随机变量函数的求法几乎一样。

换句话说，若是把实题练得非常熟练，凭仗历年实题中的类似题型就能在2020年的测验中拿到更高129分。

三、得出结论从上述阐发中，可见实题的重要性。实题的复现率很高，是最有价值的习题册。复习中，应越早训练实题越好，训练的遍数越多越好。

当你实正做完各类xxx题、冲刺x套卷等习题和模仿题后，会发现只要实题的难度是最得当的，其他题库中很大比例的题，要么简单、要么太难、要么综合性不敷。以至有的标题问题难到让人瓦解，看谜底都看不大白思绪，平白做了良多无用功。所以说，实题的标题问题量量远超任何题库。

每年的数一实题有23道摆布，30多年就是690余道，加上数二数三中不异范畴的标题问题，共1000多道合适训练的好题，数量和题型足够。

实题是一个近在手边的宝藏！良多同窗晓得那个事理，但在现实中却往往不敷重视实题。

为什么？

因为很多人选择的战略是先苦后甜，老是喜好把好工具留到最初享用，认为要先到达必然程度后再训练实题，认为太早做实题会浪费实题的价值。成果，曲到10月前不断都在做其他习题，10月后渐渐做上一遍实题就上考场了。各类标题问题却是做了很多，但量量不敷，且做得泛而不精！对常识框架和思维定势的培育其实不到位。

实题的价值只考前过一遍就能闪现出来吗？那也是影响最末考研成就的一个重要的认识不合！通过实题，一方面可提炼、熟悉常考题型，另一方面可完美常识框架和思维定势。那都是需要频频、多轮、深切研究实题才气做到的！

正所谓，滴水能穿石，铁杵磨成针，专一的力量是强大的！

举个例子，2020年数一第3题（标题问题见下文）。看选项求的都是二重极限，在思维中马上调出常识框架，二重极限的求法有如下办法：①化简（四则、等价无限小代换、根式有理化、提非零因子，等等）；②操纵“无限小量×有界量=无限小量”； ③夹逼定理；④通过变量替代,转化为一元函数极限；⑤操纵可微的充要前提求特定形式的极限。好，挨个儿把那五个办法都试验一边，快速排除不成能的，最末必然有一个办法好使！那就是成立在完美常识框架上的穷举法。练实题到达必然境界后，碰到问题，思维中各类常识框架、思维定势背得纯熟，信手拈来，那才算出师。

选最棒的标题问题，做最精的训练！

进入强化阶段以后，若是你起头复习比力晚，那么实题更应放在前面，做为主力训练题，其他习题册和模仿题册应放在后面，做为弥补训练，会更有效一些。那种复习战略可能与良多人的认知不符，但出格合适那些复习时间不敷用的同窗。

无论若何选择训练标题问题，拿笔算一下时间，xxx题做完要用几个月？实题做完要用几个月？做个时间表，在考前给实题预留下足够的时间！

下面是一些小小的战术细节：

若是你在9月初还在做各类各样的习题，还没起头啃实题，更好尽快起头啃，实题值得频频啃到测验前夜；若是实题只啃一边，一个月后印象会变淡，以至连思绪可能都记不起了，只记得曾经做过。所以，每一道实题都值得频频揣测三遍以上，更大程度强化记忆；若是你的实题书很薄弱，只要10或15年，更好花点钱，买一本更全年份的，30多年的更好了；若是你的实题书不是分类、分题型解析的，更好再花点钱，买一天职类解析的，有利于归纳题型；若是你啃完一套只要单一解法的习题书，无妨换一套以多种解法为特点的实题书再啃一边；若是你已经啃了三遍以上实题，无题可做时，能够买其他类此外不异范畴的实题来做（好比考数一的买数二数三来做），绝对会大有裨益。若是啃分类题型时，为了细嚼慢咽而放慢了节拍，能否能够考虑在冲刺阶段用套卷来训练速度？提早适应考场节拍？

当上述那些 “精练” 都做完以后，再回头来看，本身的程度是不是扎扎实实地进步到了让本身都惊讶的地步？踏上考场时，还会担忧本年标题问题难吗？

四、附上2020年数学一实题的超详细解析（可能是最详尽的解析）

数二、三统计后续发，可存眷同名公号，之前发过一篇辅导教材的评测，7月中下旬会发一篇关于实题辅导书的评测和关于实题解题思维的文。暑假会在知乎曲播，研究实题及其背后的常识框架。

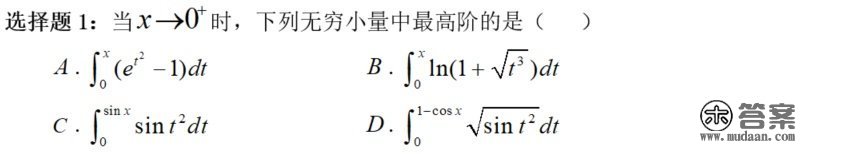
【阐发】开门见“山”，开卷就碰到一道貌似很复杂的题，搞不定的话会压力山大。碰到少见题型，怎么办？常识框架+思维定势！先在思维中的常识框架中搜刮相关考点，“无限小量中更高阶”显然是考“无限小阶的比力”嘛，OK，那是一个求除式极限的问题，马上想到用“洛必达法例”上下同时求导，并且四个选项都是变上限积分函数，立马思维定式：碰到变上限积分，先求导再说！那么思绪有了吧，无限小量比力+洛必达法例+变上限积分求导，动笔……

【总结】带有变上限积分的无限小量比力问题，多年未考了，若是只做近15年实题，可能会遗憾错过。所以，建议买一本20年或30年的更全的实题，早期题的重现率比来几年有所上升。

【难度】★★☆☆☆

【立异】★★★☆☆

【类似实题】类似度：高

【阐发】题干没太多有用信息，看选项都是围绕“可导”。 A,BA,B 是可导的充实前提，属于“操纵导数定义判断可导性”类题型； C,DC,D 是可导的需要前提，属于“操纵导数定义求极限”类题型。别的，选项中带有根号和绝对值，应与极限存在的充要前提有关。

【总结】凑导数定义时，先添项凑出尺度形式，再补项使之恒等。常考题型，不该失分。

【难度】★★☆☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高

【阐发】先看四个选项，求的都是二重极限，马上挪用常识框架，二重极限的求法有：①化简（四则、等价无限小代换、根式有理化、提非零因子，等等）；②操纵“无限小量×有界量=无限小量”； ③夹逼定理；④通过变量替代,转化为一元函数极限；⑤操纵可微的充要前提求特定形式的极限。

按理来说，要挨个儿把那五个办法都试验一边，但标题问题前提给了“可微”，能够做出合理揣度：应该是操纵了可微的充要前提来计算极限。前提还给出了 (0,0)(0,0) 点的法向量，以及切平面上的某向量。先把每个选项的点乘和叉乘展开再说。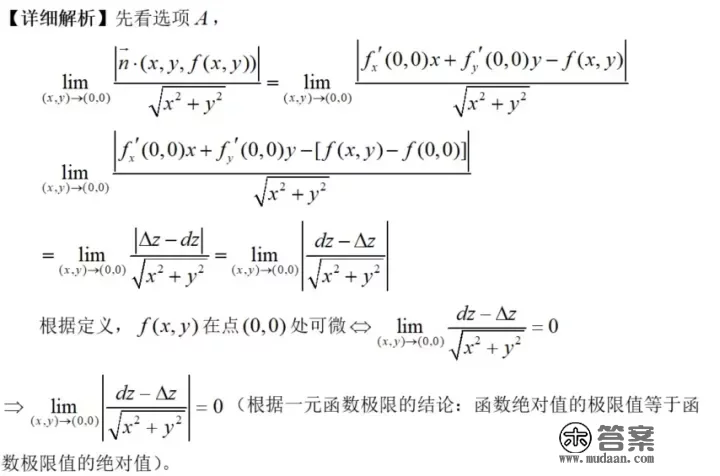

【难度】★★★☆☆

【立异】★★★★☆

【总结】本题考点：向量代数+可微的定义+函数绝对值的极限。其实本题不消做，就能间接看出谜底来！因为 B,DB,D 选项都是求向量外积的模，那个求起来计算量太大了，选项 CC 是内积，但却该向量又没详细给出，所以只可能是 AA 。当然为了保险起见，验证一下 AA

的准确性就行了。

【类似实题】类似度：中

【阐发】起首，发现变量换了个写法——把常见的幂级数的 xx 间接换了个写法 rr ，其实是为了求新而求新啊。察看标题问题，已知收敛半径，要求相关区间的敛散性问题，马上反响出那是一个关于阿贝尔定理的问题。

【总结】考察对收敛半径定义掌握的准确水平，那种问题的关键在于 ±R\pm R

处点的收敛性。

【难度】★★☆☆☆

【立异】★★★☆☆

【类似实题】类似度：中

【阐发】一打眼就是考察矩阵的有关初等变更的定理，很容易得出谜底。

【总结】常考题型，很简单。

【难度】★☆☆☆☆

【立异】★★☆☆☆

【类似实题】类似度：高

【阐发】“订交于一点”那个前提能推出什么结论呢？就是联立两个方程，但那个方程是点向式的，转化为参数式才便利联立。选项都是关于线性相关性和线性表出的，操纵定义，找出关系即可。

【总结】空间解析几何与线性代数连系的题型，考察的内容其实不深切，但需要准确变更才气得到成果。

【难度】★★☆☆☆

【立异】★★★☆☆

【类似实题】类似度：高

【阐发】那类概率题的思绪就是算一步看一步，算到中间某步，会用到已知前提，得出成果。别的，此类题，有个思维定势：看到 P(AB)=0 ，一般会有 AB 的一个子集，其概率为 0 。

【总结】事务的运算+概率的性量。留意，标题问题中呈现概率为 0 或 1

的时候，必然要加以操纵。

【难度】★★☆☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高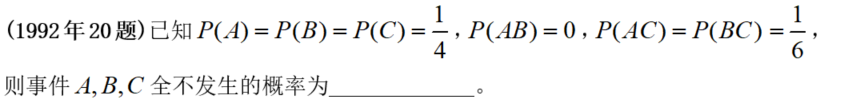

【阐发】本题间接考察中心极限制理，能够间接背公式，也能够记住原理，现场推导。

【难度】★☆☆☆☆

【立异】★★★☆☆

【总结】大数定律和中心极限制理的公式，建议双管齐下，既死记硬背，又记牢原理，忘了也能分分钟推导出来。那么多年以来第一次在数一中考察大数定律，但数三曾屡次考过。

【类似实题】类似度：高

【阐发】先间接代入，是\infty-\infty 型，再挪用常识框架，该类型的处置办法凡是有四种：①通分；②有理化；③提因子；④变量代换（尤其是倒代换）。此题是分式，故通分。接下来，进一步化简，化到不克不及再化简后，运用洛必达法例，搞定。

【总结】送分题，要包管准确率。

【难度】★☆☆☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高

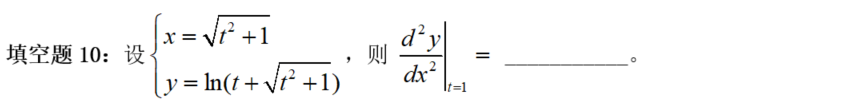
【阐发】参数方程求二阶导的题型。代入公式间接求即可。

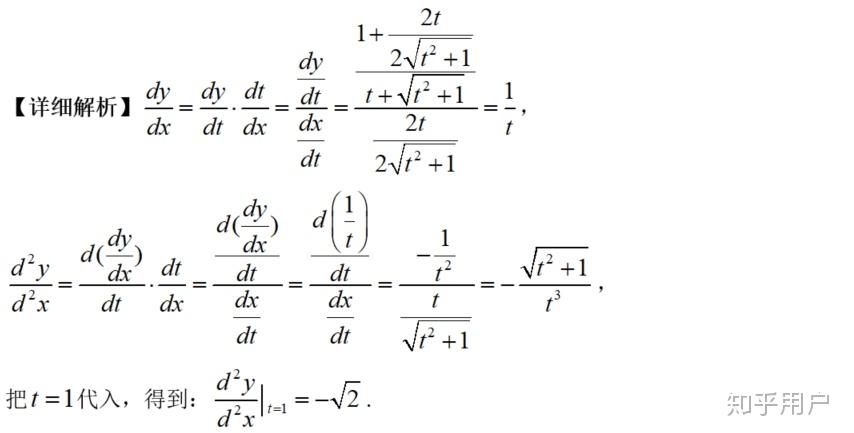
【总结】送分题，必拿分。

【难度】★☆☆☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高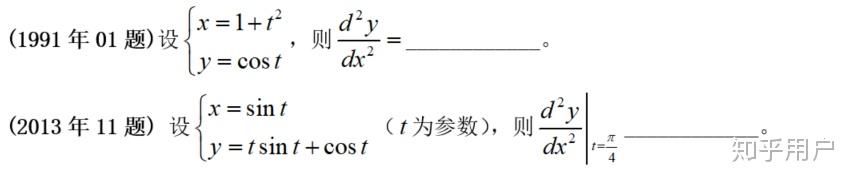

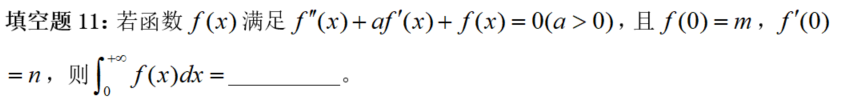
【阐发】属于稀有题型，没什么套路，所以用“前提结论阐发法”。看前提，有个高阶微分方程，马上想到可能要求通解；再看结论，是个广义积分，求出原函数，代入极限即可，但关键是：笼统函数求不出原函数啊！所以，笼统函数只能笼统来算，找笼统关系式。前提中正好有一个关系式，能够代入尝尝，正好能求出原函数。

【总结】本题确实又新颖又难，需要讨论，计算量比力大，会耗时6-10分钟。16年曾经呈现过一次类似题型，若是对实题熟悉，最最少会有思绪！

【难度】★★★★★

【立异】★★★★☆

【类似实题】类似度：高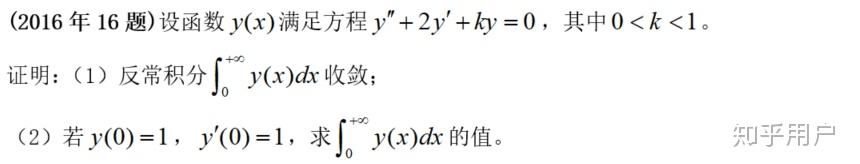

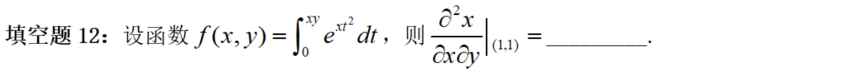
【阐发】那是个常见题型——被积函数同时含有上限变量 x 和积分变量 t 的变限积分的求导。但又有所立异，又连系了混合偏导数的计算。起首，把那个变限积分求出来，操纵常识框架，核心思惟是让被积函数中只含有积分变量，而不含。又分为两种情况：①情形一：被积函数中的可别离，则把含的表达式提到积分号外。②情形二：被积函数中的不成别离，则需要做换元处置。此题显然属于情形二，要做换元。

【总结】一道很新颖的“混合了上限的变上限积分”+“混合偏导数计算”标题问题。

【难度】★★★☆☆

【立异】★★★★☆

【类似实题】类似度：中

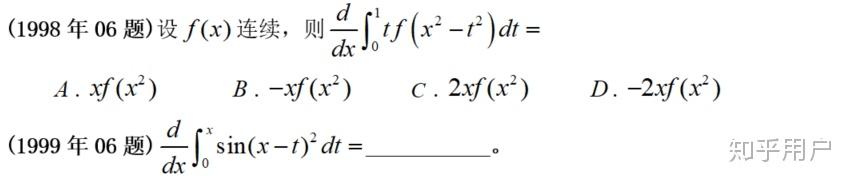
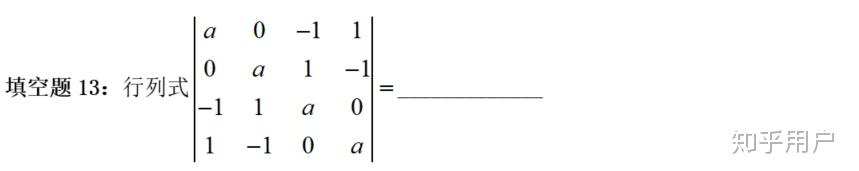
【阐发】操纵常识框架，数值型行列式有两类解题思绪：(1)操纵行列式的性量，将所求行列式化简，凡是转化为上述几类特殊特殊行列式(尤其是上下三角行列式)或变形出尽可能多的零元素；(2)操纵行列式展开公式，把行列式的阶数降低（有时会用到递推法）。凡是那两类解题思绪能够共同利用。

关于低阶行列式，先操纵行列式的性量，变形出尽可能多的零元素，更好是某一行只含1或2个零元素，于是就能够按那一行展开，转化为三阶行列式，而三阶行列式是有公式的。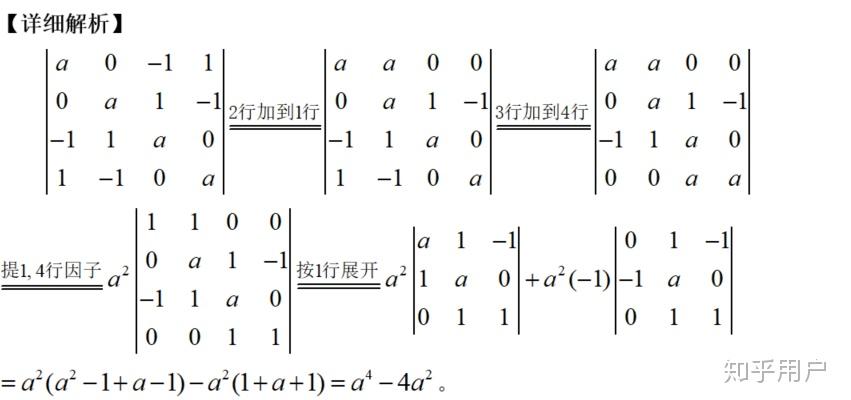

【总结】低阶数值型行列式

的处置办法要心中有数。当然本题操纵性量化简还有良多种解法。

【难度】★☆☆☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高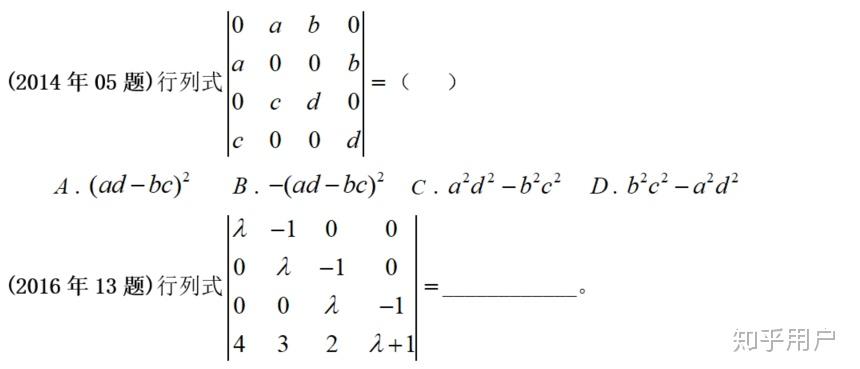

【阐发】本题考察协方差的性量和计算，其实不难，中间步调必定会用到求随机变量的期望或随机变量函数的期望。

【总结】协方差公式

+期望计算。

【难度】★★☆☆☆

【立异】★★☆☆☆

【类似实题】类似度：中

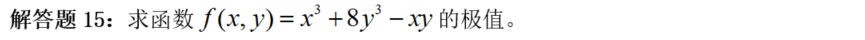
【阐发】一道十分尺度的多元函数求无前提极值问题，十分简单。操纵常识框架，需要前提求范畴，充实前提再挑选。

【总结】送分题，要包管准确率。

【难度】★☆☆☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高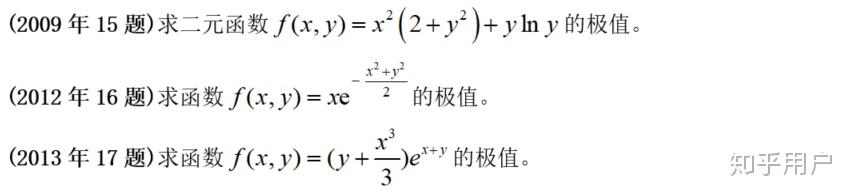

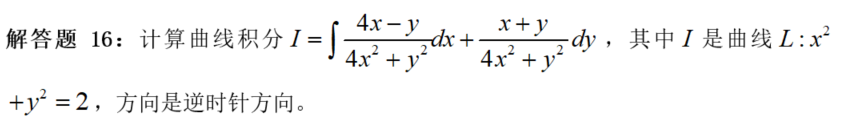
【阐发】操纵常识框架，第二类曲线积分的计算有“三大根底性办法”(包罗间接计算、格林公式、积分与途径无关定理)和“两小技巧性办法”（包罗曲线方程代入被积函数、对称性）。简单验算一下，发现 \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} 为零，故我们选用格林公式。但要留意格林公式的前提，一曲直线 L 必需封锁且正向；二是 P(x, y), Q(x, y), \frac{\partial Q}{\partial x}, \frac{\partial P}{\partial y} 那四个函数在平面闭区域 D 上必需持续。本题满足第一条，但不满足第二条，有一个不持续点 (0,0) ，该点处分母是零。响应的处理办法是“挖洞法”，且按照分母形式来找“洞”，即找一个小封锁曲线 4 x^{2}+y^{2}=\varepsilon^{2} ，使得积分容易处置。

【总结】那是一道十分典型、常见的考题，以至和一些辅导书的原题几乎一模一样，那个分数应该是必拿的，但此题独一的难处在于计算量，若是不纯熟的话，用时会超出均匀时间。

【难度】★★★☆☆

【立异】★☆☆☆☆

【类似实题】类似度：高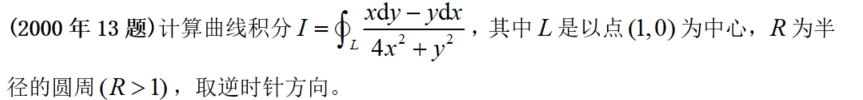

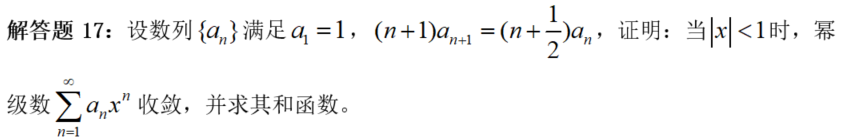
【阐发】先证明后计算。认真阅读那个证明题，其实也是一个求幂级数的收敛区间的计算题。操纵常识框架，马上想到求收敛半径的两种手段：一是一般幂级数 \sum_{n=0}^{\infty} u_{n}(x) 情形（可能出缺项）；二是尺度幂级数 \sum_{n=0}^{\infty} a_{n} x^{n} 情形（不缺项）。本题那两种手段都能够，我们用第一种。用比值法 \lim _{n \rightarrow \infty} \frac{\left|u_{n+1}(x)\right|}{\left|u_{n}(x)\right|}=\rho(x) ，令

【总结】本题用到的微分方程法，但历年考研中也曾几次考察过，若是对实题熟悉，思绪应该能想到，但本题算是此中最难的，因为需要本身找到关系式！本题次要难在那儿！

【难度】★★★★☆

【立异】★★★★☆

【类似实题】类似度：高

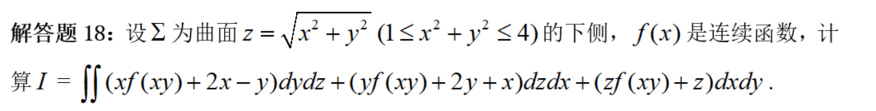
【阐发】挪用常识框架，第二类曲面积分的计算有如下办法：三大根底性办法”（包罗间接计算、合一投影法、高斯公式）和“两小技巧性办法”（包罗曲线方程代入被积函数、对称性）。此中，被积函数中含有笼统函数招致高斯公式利用未便，且分面投影的间接计算法也不成行，所以，能够锁定处理办法为：合一投影法。合一投影法素质上是操纵两类曲面积分之间的关系，先转化为第一类曲面积分，再转化为某一坐标面上的二重积分。

【总结】关于第二类曲面积分，历年考研大多考察高斯公式，但本题另辟门路，被积函数是笼统函数

，合适用合一投影法。只要思绪有了，会发现现实计算其实不难。

【难度】★★☆☆☆

【立异】★★★★☆

【类似实题】类似度：高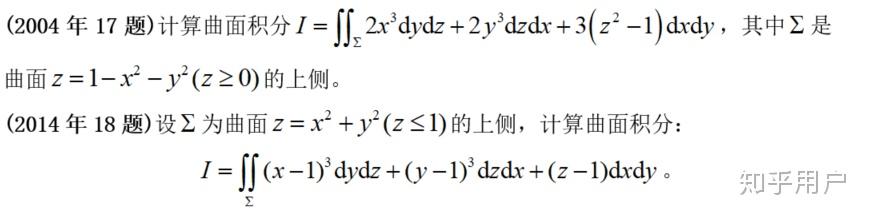

【阐发】察看第（1）问，含有一个中值的导数，能够阐发出本题应该用到拉格朗日中值定理。本题给了三个点 x=0,2 以及使得 \left| f(x) \right| 取到更大值 M 的 x_{0} ，那么必定应该是在那三个点构成的两个区间上别离应用中值定理。第（2）问属于出格难那种证明题。结论中含有 \forall ，故可考虑用反证法。

【总结】本题第一问中规中矩不算难，拉格朗日套用上，讨论一下就行了，做不出来只能怪本身根底不老了。但第二问是证明题中的难题，把拉格朗日和莱布尼茨公式连系起来用，那种思绪很难想到，所以那5分其实不克不及强求。

【难度】★★★★★

【立异】★★★★☆

【类似实题】无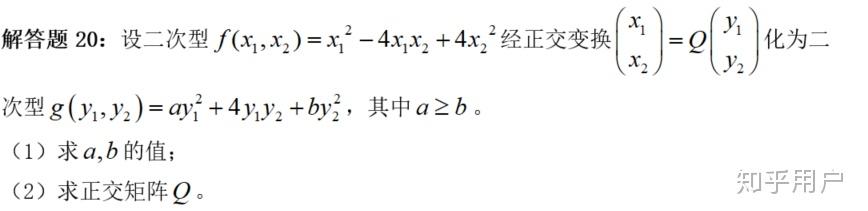

【阐发】本题比力新颖， A 经正交变更到 B ，两个二次型矩阵是什么关系？要熟悉原始的推导过程： f(x)=x^{T} A x=(Q y)^{T} A(Q y)=y^{T}\left(Q^{T} A Q\right) y=y^{T} B y=g(y) ，可见，两个二次型矩阵的关系是：既合同 B=Q^{T} A Q 又类似 B=Q^{-1} A Q （因为 Q 是正交矩阵）。通过合同和类似的一些性量，就能求出系数。第二问求正交矩阵，那个需要转换思绪，我们只会求 A \rightarrow \Lambda 和 B \rightarrow \Lambda \text {} 时的正交矩阵，但因为 A,B 类似，有不异的特征值，故都可化为统一个对角矩阵 \Lambda ，所以别离求出两个正交矩阵，通过 \Lambda 得到关系式，最初变更为 B=Q^{T} A Q 的形式，即可得到成果。

【总结】第一问是两个矩阵类似，操纵性量求矩阵中的未知量，与2015年和1998年的实题十分类似。第二问是求 P^{-1} A P=B 中的可逆矩阵 P

，那与2015年的第二问类似但有一些不同。与其解题思绪一致的是2002年的第三问。

【难度】★★★☆☆ 中等

【立异】★★★★☆ 比力新颖

【类似实题】类似度：中

【阐发】操纵常识框架，矩阵可逆的证明办法常用的有：①定义；②行列式不为零；③ r(A)=n ；④行（列）向量组线性无关；⑤构成的方程组有独一解；⑥特征值全不为零；⑦ A^{T} A 是正定矩阵。挨个试一下，本题中前提比力少，并且不是详细向量，所以我们选择④，判断列向量组能否线性无关。用线性无关的定义，连系已知前提，很容易证得。第二问较难一些，良多同窗卡在了开头的关键思绪上，此题最关键的思绪是：因为矩阵是笼统的，其逆矩阵求不出，所以若求 B=P^{-1} A P ，只能做变形处置，即 P B=A P 。那是个常见的处置办法，特征值、特征向量的求法就来源于此。