请简明扼要地说明BARRA模型能用来做什么？如果要用python实现，如何建立框架？
我来尝尝因子计算 0.布景
2018年，MSCI发布了最新的中国权益市场风险模子The Barra China Equity Model，即CNE6。但是，至今为行，无人在收集上发布因子计算代码。所以，我筹算写一个系列文章，操纵Python脱手复现CNE6因子计算。
CNE6因子以因子表露的形式呈现。如下图所示，我们用“时间-股票代码-因子表露值”的形式保留我们算得的因子数据。数据格局1.筹办工做 1.1.数据“巧妇难为无米之炊”。要计算因子，则必需筹办好用于计算的底层数据。我接纳聚宽做为数据源，搭建了底层数据库，并编写了数据挪用的接口。
JoinQuant聚宽量化交易平台www.joinquant.com/为便利计算，数据颠末了一些处置。关于日频数据，以time（时间）和code（代码）为固定列；关于季频数据，则以code（代码）、statDate（统计日期）、pubDate（公布日期）为固定列。日期均利用datetime格局，代码均利用object格局。
日频数据格局季频数据格局下面展现我本身编写的数据接口函数，和聚宽数据接口十分类似，用于大量挪用本身保留好的底层数据，请各人不要混淆！列位能够按照本身的现实需求，决定能否需要复现。
1.1.1.获取行情数据（get_price）
该函数默认获取比来250个交易日，所有股票的后复权的OHLCV数据，获取的字段能够自定义。底层数据包罗所有股票、指数的行情。底层数据获取办法见聚宽api文档：
https://www.joinquant.com/help/api/help#Stock:获取行情数据www.joinquant.com/help/api/help#Stock:%E8%8E%B7%E5%8F%96%E8%A1%8C%E6%83%85%E6%95%B0%E6%8D%AE def get_price(codes=all-stock, start_date=None, end_date=None, count=250, fq=post, fields=None, mode=history, filter=None): """ codes: list,或者,all-stock取所有股票,all-index取所有指数。 start_date, end_date:str %Y-%m-%d or %Y%m%d count: 交易日数量。 fq: 复权。post后复权; None不复权; e-pre等比前复权。默认后复权。 fields:可取[open, high, low, close, volume, money, pre_close] mode: history or current, history形式下只挪用汗青数据，current形式下挪用外部数据补全数据。 - history形式适用于战略研究，无需外部数据源； - current形式适用于实战，盘中获得最新数据实时运行战略。 filter: 自定义过滤器 """ ... get_price函数运行成果1.1.2.获取估值数据（get_valuation）
该函数默认获取比来250个交易日，所有股票的估值数据。该数据源自于聚宽的valuation表格，数据获取办法，字段解释等见聚宽api文档：
https://www.joinquant.com/help/api/help#Stock:市值数据www.joinquant.com/help/api/help#Stock:%E5%B8%82%E5%80%BC%E6%95%B0%E6%8D%AE def get_valuation(codes=None, start_date=None, end_date=None, count=250, fields=None, filter=None): """ 获取股票的估值数据。 codes: list股票代码列表；默认None获取所有股票数据； start_date, end_date: str %Y-%m-%d or %Y%m%d 或者 datetime 格局； count: int, 所取数据的交易日的数量，默认比来250个交易日； fields: list, 数据字段，默认全取。 filter: 自定义过滤器 """ ... get_valuation函数运行成果1.1.3.获取交易日（get_trade_date）
该函数能够获取一段时间的交易日。start_date, end_date, count三个参数肆意给定两个，则返回对应的交易日。
def get_trade_date(start_date=None, end_date=None, count=None): """ 获取一段时间内的交易日。 start_date:起头日期，datetime格局或者str格局 end_date:完毕日期，datetime格局或者str格局 count:数量，int 若是三个参数都给出，默认利用start_date和end_date参数。 """ ... get_trade_date函数运行成果1.1.4.获取股票行业（get_industry）
该函数能够获取股票所属行业。给定日期、股票代码列表、行业类别列表，则能返回一个包罗索取信息的DataFrame。底层数据源自于聚宽的get_industry函数：
https://www.joinquant.com/help/api/help#Stock:获取行业、概念成份股www.joinquant.com/help/api/help#Stock:%E8%8E%B7%E5%8F%96%E8%A1%8C%E4%B8%9A%E3%80%81%E6%A6%82%E5%BF%B5%E6%88%90%E4%BB%BD%E8%82%A1 def get_industry(codes=None, date=None, industry_type=None): """ 获取股票所在行业。 codes: list, 股票代码； date: 日期 industry_type: 行业分类类型。 - [sw_l1, sw_l2, sw_l3, zjw, jq_l1, jq_l2] - 别离对应申万L1/L2/L3、证监会、聚宽L1/L2 """ get_industry函数运行成果1.1.5.获取根本面数据（get_basic）
该函数能够获取股票三大报表数据和财政目标数据，并可以根据指定的聚合办法计算TTM目标。底层数据来自聚宽的4个表格：balance、cash_flow、income、indicator。详细数据提取办法、字段申明见聚宽文档：
https://www.joinquant.com/help/api/help#Stock:资产欠债数据
https://www.joinquant.com/help/api/help#Stock:现金流数据
https://www.joinquant.com/help/api/help#Stock:利润数据
https://www.joinquant.com/help/api/help#Stock:财政目标数据
def get_basic(codes=None, start_date=None, end_date=None, count=4, fields=None, ttm_dict={}): """ 股票财政数据并表查询函数。获取数据后主动合并报表。 codes: 股票代码，list，默认获取全数。 start_date/end_date: 起头和完毕日期，默认为空。 count: 默认为4，代表取比来4个季度的数据。 fields: 相关字段，默认不取。能够利用`get_field_descrition`获取字段申明。 ttm_dict: 需要计算ttm的字段（keys）、ttm聚合办法（values）构成的dict。构造如下。 - {ttm_field1: agg_method1, ttm_field2: agg_method2, ...} - 常用的TTM聚合办法有[mean, sum, last, ...]或者自定义函数，可操做长度为4的Series。 - ttm_dict和fields是取并集的，也即在此呈现的字段，将主动合并至fields。 """ get_basic函数运行成果1.2.参考材料CNE6的计算公式、计算办法次要参考渤海证券
的研报，因为我没找到MSCI的原文。渤海证券研报的下载地址为：
《Barra 风险模子（CNE6）之单因子检测——多因子模子研究系列之八》 http://download.hexun.com/ftp/yanbao2018/20190621/V+cgE328aSA1o7COWFMehA.PDFdownload.hexun.com/ftp/yanbao2018/20190621/V+cgE328aSA1o7COWFMehA.PDF《Barra 风险模子（CNE6）之纯因子构建与因子合成——多因子模子研究系列之九》
http://pg.jrj.com.cn/acc/Res/CN_RES/INVEST/2019/6/20/92fd68e8-bd61-4c86-a0d9-20c6351b968f.pdfpg.jrj.com.cn/acc/Res/CN_RES/INVEST/2019/6/20/92fd68e8-bd61-4c86-a0d9-20c6351b968f.pdf以及，《Barra Risk Model Handbook》。
https://roycheng.cn/files/riskModels/barra_risk_model_handbook.pdfroycheng.cn/files/riskModels/barra_risk_model_handbook.pdf 1.3.一些小寄巧1.3.1.快速大量OLS
在气概因子的计算过程中，经常需要利用线性回归。假设我们有如许一个线性回归方程：
y=Xβ+εy=X\beta+\varepsilon \\
我们已知自变量XX和因变量yy，需要估量参数β\beta。则参数β\beta能够被计算为：
β=(XTX)−1XTy\beta=(X^TX)^{-1}X^Ty \\
而在现实中，那个运算过程可能要停止良多次。好比，假设我们需要滑动窗口停止时间序列回归，估量股票的beta（市场因子风险表露），则每个交易日、每只股票都要停止一次运算。那么比来一年，每日beta就需要计算100万次以上。若是挪用已经封拆好的第三方库，估量要算到明年……
但我们留意到，市场因子收益率在统一个交易日连结稳定（即XX在统一个交易日连结稳定），只是差别的股票有纷歧样的股票收益率序列（上式中只要yy在变革）。所以我们将股票收益率序列横向拼接成收益率矩阵YY，即可在截面上一次性估量所有股票的beta，构成beta矩阵BB：
B=(XTX)−1XTYB=(X^TX)^{-1}X^TY \\
要估量去除市场因子外的残差收益率，则只需要将BB矩阵代回上式：
E=Y−XBE=Y-XB \\
在Python中，上述过程只需要通过Numpy即可实现：
import numpy as np X, Y = ... # 参加常数项 X = np.c_[np.ones(X.shape[0]), X] # 那里利用伪逆，制止矩阵不满秩带来的错误 B = np.linalg.pinv(X.T@X)@X.T@Y E = Y - X@B1.3.2.加权回归WLS
在CNE6的因子计算过程中，往往需要我们利用加权回归来估量参数，以包管比来的样本有较大的权重。在Barra手册中，定义了指数加权的办法。Barra起首定义了一个参数λ\lambda，该参数由半衰期（half-life）控造：
λ=(0.5)1/half−life\lambda=(0.5)^{1/\mathrm{half-life}} \\
关于时间点tt，样本权重则被计算为：
w(t)=λT−tw(t)=\lambda^{T-t} \\
加权最小二乘估量的原理能够参考此篇博客，讲的十分明晰：
加权最小二乘法与部分加权线性回归236 附和 · 11 评论文章我们从中获取了加权最小二乘回归参数估量表达式：
β=(XTWX)−1XTWy\beta=(X^TWX)^{-1}X^TWy \\
此中， W=\mathrm{diag}(w_{1},\dots, w_t, \dots,w_T )，是一个对角阵，包罗每个样本的权重。留意，那里的权重之和不需要为1，那是因为：
tr(W)=T∑t=1wt
\mathrm{tr}(W)=\sum_{t=1}^T w_t \\我们令矩阵V=\frac{1}{\mathrm{tr}(W)}W，是一个尺度化后的权重矩阵。则β\beta的计算办法是一样的：
\beta=(X^TVX)^{-1}X^TVy\\=(\frac{1}{\mathrm{tr}(W)}X^TWX)^{-1}X^T\frac{1}{\mathrm{tr}(W)}Wy \\=(X^TWX)^{-1}X^TWy \\
有了以上那些根底，我们在Python中实现带半衰期的加权最小二乘回归：
import numpy as np # 定义窗口大小、半衰期 window, half_life = 252, 63 L, Lambda = 0.5**(1/half_life), 0.5**(1/half_life) W = [] for i in range(window): W.append(Lambda) Lambda *= L W = np.diag(W[::-1]) # 加权最小二乘回归 X, y = ... beta = np.linalg.pinv(X.T@W@X)@X.T@W@y 2.市值因子（Size） 2.1.因子定义Size（一级因子） Size（二级因子） LNCAP（三级因子）: 规模。畅通市值的天然对数。Mid Cap（二级因子） MIDCAP（三级因子）: 中市值。起首取 Size 因子表露的立方，然后以加权回归的体例对 Size 因子正交，最初停止去极值和尺度化处置。根据渤海证券的研报中申明，此处的加权回归是指横截面回归，权重为市值开根号。而此处的去极值为MAD办法，接纳5倍MAD去除极端值。
2.2.代码实现起首，我们运用数据获取函数获取股票每个交易日的市值，单元为亿元。数据构造展现如下。
然后，实现MAD去极值办法：
def MAD_winsorize(x, multiplier=5): """MAD去除极端值""" x_M = np.nanmedian(x) x_MAD = np.nanmedian(np.abs(x-x_M)) upper = x_M + multiplier * x_MAD lower = x_M - multiplier * x_MAD x[x>upper] = upper x[x<lower] = lower return x然后，实现因子计算：
def cal_Size(codes=None, start_date=None, end_date=None, count=250): def __reg(df): y = df[sub_MIDCAP].values X = np.c_[np.ones((len(y), 1)), df[LNCAP].values] W = np.diag(np.sqrt(df[circulating_market_cap])) beta = np.linalg.pinv(X.T@W@X)@X.T@W@y # 去除极端值 resi = MAD_winsorize(y - X@beta, multiplier=5) # 尺度化 resi -= np.nanmean(resi) resi /= np.nanstd(resi) return pd.Series(resi, index=df[code]) # 获取数据 tmp = get_valuation(codes=codes, start_date=start_date, end_date=end_date, count=count, fields=[circulating_market_cap]) # 第一个三级因子 tmp[LNCAP] = np.log(tmp[circulating_market_cap]+1) tmp[sub_MIDCAP] = tmp[LNCAP]**3 # 截面回归正交化处置 MIDCAP = tmp.groupby(time).apply(__reg) MIDCAP.name = MIDCAP tmp = tmp.merge(MIDCAP.reset_index()) #tmp[Size] = (tmp[LNCAP]+tmp[MIDCAP])/2 return tmp[[code, time, LNCAP, MIDCAP]]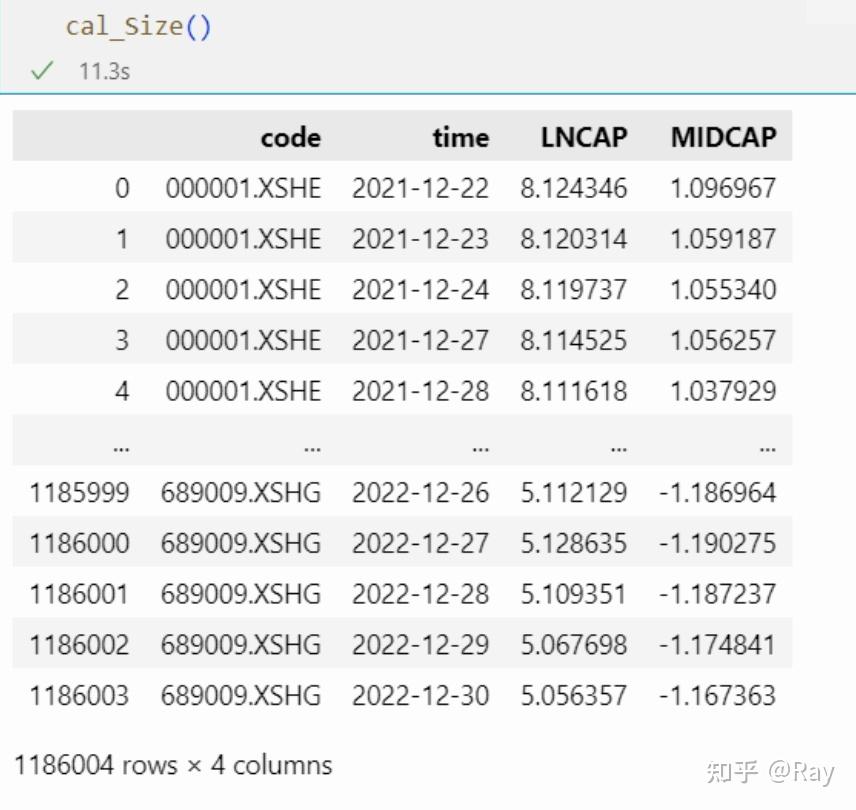
3.颠簸率（Volatility）
3.1.因子定义
Volatility（一级因子）
Beta（二级因子） BETA（三级因子）:股票收益率对沪深 300 收益率停止时间序列回归，取回归系数，回归时间窗口为 252 个交易日，半衰期 63 个交易日。r_t=\alpha+\beta R_t+e_t \\
Residual Volatility（二级因子） Hist sigma（三级因子）:在计算 BETA 所停止的时间序列回归中，取回归残差收益率的颠簸率。Daily std（三级因子）:日收益率在过去 252 个交易日的颠簸率，半衰期 42 个交易日。Cumulative range（三级因子）: 累计收益范畴（按月收益计算）,计算办法见下方。Z(T)为过去T个月的累计对数收益率（每个月包罗21个交易日），即：
Z(T)=\sum_{\tau=1}^{T} \ln (1+r_{\tau}) \\
此中，r_\tau是股票在\tau月的收益，T=1, \dots, 12，从而定义累计收益范畴目标计算表达式：
\mathrm{CMRA}= \max(Z(T))- \min(Z(T)) \\
3.2.代码实现 3.2.1.数据筹办起首，我们提取所有股票的收盘价、前收盘价，沪深300指数的收盘价、前收盘价，然后计算出所有股票和沪深300每个交易日的收益率。此处函数__start_end_date__是一个转化函数，将start_date、end_date、count三个参数转化为start_date、end_date两个参数。那个函数由前文的get_trade_date函数衍生而来。（仿佛有些复杂化了……）
import pandas as pd codes=None start_date=None end_date=None count=250 window=252 half_life=63 if codes is None: codes = all-stock s, end_date = __start_end_date__(start_date=start_date, end_date=end_date, count=count) start_date, _ = __start_end_date__(start_date=None, end_date=s, count=window) price = get_price(codes=codes, start_date=start_date, end_date=end_date, count=count, fields=[pre_close, close]) hs300 = get_price(codes=[000300.XSHG], start_date=start_date, end_date=end_date, fields=[pre_close, close]) price = pd.concat([price, hs300]).reset_index(drop=True) price[ret] = price[close] / price[pre_close] - 1 price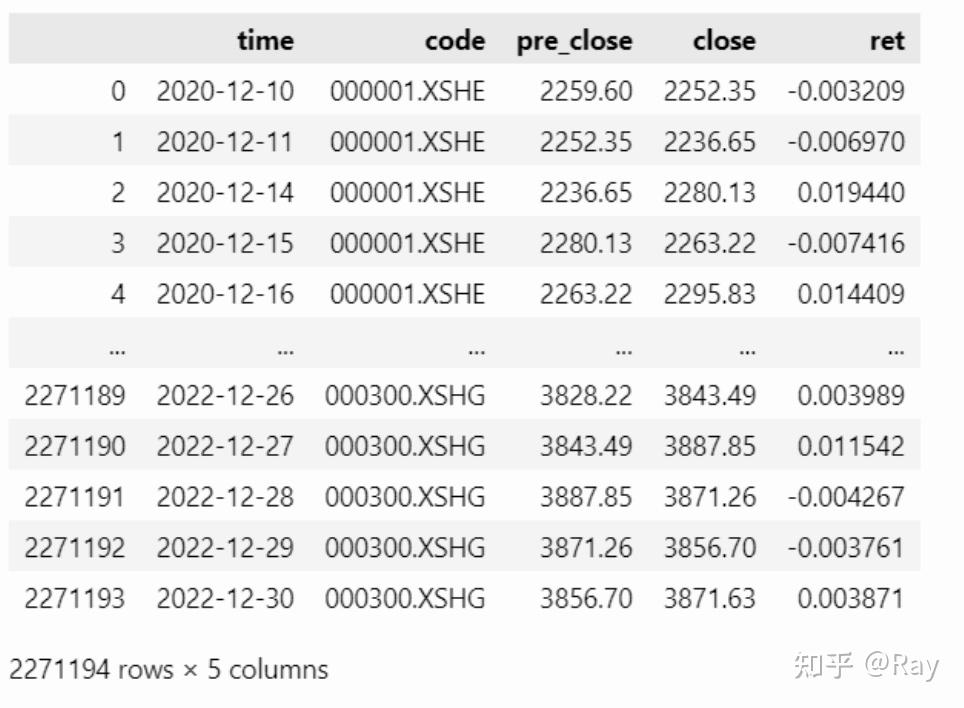
3.2.2.BETA和Hist sigma
然后，我们实现BETA和Hist sigma因子的计算。留意到，股票收益率数据存在缺失值，那将招致回归参数估量失败（矩阵运算成果为NaN）。所以，在肆意交易日，我们挑选出具有完好数据的股票，停止批量的加权最小二乘估量；而不具有完好数据的股票，则别离取出，将数据对齐，再停止参数估量。若是比来252个交易日内，股票样本点少于63个，则不停止估量。
from rich.progress import track from IPython.display import clear_output ret = pd.pivot_table(price, values=ret, index=time, columns=code) L, Lambda = 0.5**(1/half_life), 0.5**(1/half_life) W = [] for i in range(window): W.append(Lambda) Lambda *= L W = W[::-1] # 计算BETA和Hist_sigma beta, hist_sigma = [], [] for i in track(range(len(ret)-window+1), description=正在计算beta...): tmp = ret.iloc[i:i+window, :].copy() W_full = np.diag(W) Y_full = tmp.dropna(axis=1).drop(columns=000300.XSHG) idx_full, Y_full = Y_full.columns, Y_full.values X_full = np.c_[np.ones((window, 1)), tmp.loc[:, 000300.XSHG].values] beta_full = np.linalg.pinv(X_full.T@W_full@X_full)@X_full.T@W_full@Y_full hist_sigma_full = pd.Series(np.std(Y_full - X_full@beta_full, axis=0), index=idx_full, name=tmp.index[-1]) beta_full = pd.Series(beta_full[1], index=idx_full, name=tmp.index[-1]) beta_lack, hist_sigma_lack = {}, {} for c in set(tmp.columns) - set(idx_full) - set(000300.XSHG): tmp_ = tmp.loc[:, [c, 000300.XSHG]].copy() tmp_.loc[:, W] = W tmp_ = tmp_.dropna() W_lack = np.diag(tmp_[W]) if len(tmp_) < half_life: continue X_lack = np.c_[np.ones(len(tmp_)), tmp_[000300.XSHG].values] Y_lack = tmp_[c].values beta_tmp = np.linalg.pinv(X_lack.T@W_lack@X_lack)@X_lack.T@W_lack@Y_lack hist_sigma_lack[c] = np.std(Y_lack - X_lack@beta_tmp) beta_lack[c] = beta_tmp[1] beta_lack = pd.Series(beta_lack, name=tmp.index[-1]) hist_sigma_lack = pd.Series(hist_sigma_lack, name=tmp.index[-1]) beta.append(pd.concat([beta_full, beta_lack]).sort_index()) hist_sigma.append(pd.concat([hist_sigma_full, hist_sigma_lack]).sort_index()) beta = pd.concat(beta, axis=1).T beta = pd.melt(beta.reset_index(), id_vars=index).dropna() beta.columns = [time, code, BETA] hist_sigma = pd.concat(hist_sigma, axis=1).T hist_sigma = pd.melt(hist_sigma.reset_index(), id_vars=index).dropna() hist_sigma.columns = [time, code, Hist_sigma] factor = pd.merge(beta, hist_sigma) 3.2.3.Daily stdDaily std定义为日收益率在过去 252 个交易日的颠簸率，半衰期 42 个交易日。根据我的理解，应该是接纳EWMA的办法估量股票收益率的颠簸率。EWMA办法颠簸率更新的表达式为：
\sigma_{t+1}^2=(1-\lambda)r_t^2+\lambda\sigma_t^2 \\
此中，参数\lambda=(0.5)^{1/42}。初始值\sigma_0=\mathrm{std}(r_t),为全样本的尺度差。初始值不太重要，因为跟着颠簸率不竭地更新，初始值对后续的数值影响不大。
# EWMA计算日尺度差Daily std init_std = ret.std(axis=0) L = 0.5**(1/42) init_var = ret.var(axis=0) tmp = init_var.copy() daily_std = {} for t, k in track(ret.iterrows(), description=正在计算Daily std...): tmp = tmp*L + k**2*(1-L) daily_std[t] = np.sqrt(tmp) tmp = tmp.fillna(init_var) daily_std = pd.DataFrame(daily_std).T daily_std.index.name = time daily_std = daily_std.loc[s:end_date, :] daily_std = pd.melt(daily_std.reset_index(), id_vars=time, value_name=Daily_std).dropna() factor = factor.merge(daily_std) 3.2.4.Cumulative range累计收益范畴（按月收益计算）定义如下：
Z(T)为过去T个月的累计对数收益率（每个月包罗21个交易日），即：
Z(T)=\sum_{\tau=1}^{T} \ln (1+r_{\tau}) \\
此中，r_\tau是股票在\tau月的收益，T=1, \dots, 12，从而定义累计收益范畴目标计算表达式：
\mathrm{CMRA}= \max(Z(T))- \min(Z(T)) \\
代码实现为：
close = pd.pivot_table(price, values=close, index=time, columns=code).fillna(method=ffill, limit=10) pre_close = pd.pivot_table(price, values=pre_close, index=time, columns=code).fillna(method=ffill, limit=10) idx = close.index CMRA = {} for i in track(range(len(close)-window+1), description=正在计算CMRA...): close_ = close.iloc[i:i+window, :] pre_close_ = pre_close.iloc[i, :] pre_close_.name = pre_close_.name - pd.Timedelta(days=1) close_ = close_.append(pre_close_).sort_index().iloc[list(range(0, 253, 21)), :] r_tau = close_.pct_change().dropna(how=all) Z_T = np.log(r_tau+1).cumsum(axis=0) CMRA[idx[i+window-1]] = Z_T.max(axis=0) - Z_T.min(axis=0) CMRA = pd.DataFrame(CMRA).T CMRA.index.name = time CMRA = pd.melt(CMRA.reset_index(), id_vars=time, value_name=Cumulative_range).dropna() factor = factor.merge(CMRA) 3.2.5.代码整合 from rich.progress import track from IPython.display import clear_output def cal_Volatility(codes=None, start_date=None, end_date=None, count=250, window=252, half_life=63): if codes is None: codes = all-stock s, end_date = __start_end_date__(start_date=start_date, end_date=end_date, count=count) start_date, _ = __start_end_date__(start_date=None, end_date=s, count=window) price = get_price(codes=codes, start_date=start_date, end_date=end_date, count=count, fields=[pre_close, close]) hs300 = get_price(codes=[000300.XSHG], start_date=start_date, end_date=end_date, fields=[pre_close, close]) price = pd.concat([price, hs300]).reset_index(drop=True) price[ret] = price[close] / price[pre_close] - 1 ret = pd.pivot_table(price, values=ret, index=time, columns=code) L, Lambda = 0.5**(1/half_life), 0.5**(1/half_life) W = [] for i in range(window): W.append(Lambda) Lambda *= L W = W[::-1] # 计算BETA和Hist_sigma beta, hist_sigma = [], [] for i in track(range(len(ret)-window+1), description=正在计算beta...): tmp = ret.iloc[i:i+window, :].copy() W_full = np.diag(W) Y_full = tmp.dropna(axis=1).drop(columns=000300.XSHG) idx_full, Y_full = Y_full.columns, Y_full.values X_full = np.c_[np.ones((window, 1)), tmp.loc[:, 000300.XSHG].values] beta_full = np.linalg.pinv(X_full.T@W_full@X_full)@X_full.T@W_full@Y_full hist_sigma_full = pd.Series(np.std(Y_full - X_full@beta_full, axis=0), index=idx_full, name=tmp.index[-1]) beta_full = pd.Series(beta_full[1], index=idx_full, name=tmp.index[-1]) beta_lack, hist_sigma_lack = {}, {} for c in set(tmp.columns) - set(idx_full) - set(000300.XSHG): tmp_ = tmp.loc[:, [c, 000300.XSHG]].copy() tmp_.loc[:, W] = W tmp_ = tmp_.dropna() W_lack = np.diag(tmp_[W]) if len(tmp_) < half_life: continue X_lack = np.c_[np.ones(len(tmp_)), tmp_[000300.XSHG].values] Y_lack = tmp_[c].values beta_tmp = np.linalg.pinv(X_lack.T@W_lack@X_lack)@X_lack.T@W_lack@Y_lack hist_sigma_lack[c] = np.std(Y_lack - X_lack@beta_tmp) beta_lack[c] = beta_tmp[1] beta_lack = pd.Series(beta_lack, name=tmp.index[-1]) hist_sigma_lack = pd.Series(hist_sigma_lack, name=tmp.index[-1]) beta.append(pd.concat([beta_full, beta_lack]).sort_index()) hist_sigma.append(pd.concat([hist_sigma_full, hist_sigma_lack]).sort_index()) beta = pd.concat(beta, axis=1).T beta = pd.melt(beta.reset_index(), id_vars=index).dropna() beta.columns = [time, code, BETA] hist_sigma = pd.concat(hist_sigma, axis=1).T hist_sigma = pd.melt(hist_sigma.reset_index(), id_vars=index).dropna() hist_sigma.columns = [time, code, Hist_sigma] factor = pd.merge(beta, hist_sigma) # EWMA计算日尺度差Daily std init_std = ret.std(axis=0) L = 0.5**(1/42) init_var = ret.var(axis=0) tmp = init_var.copy() daily_std = {} for t, k in track(ret.iterrows(), description=正在计算Daily std...): tmp = tmp*L + k**2*(1-L) daily_std[t] = np.sqrt(tmp) tmp = tmp.fillna(init_var) daily_std = pd.DataFrame(daily_std).T daily_std.index.name = time daily_std = daily_std.loc[s:end_date, :] daily_std = pd.melt(daily_std.reset_index(), id_vars=time, value_name=Daily_std).dropna() factor = factor.merge(daily_std) close = pd.pivot_table(price, values=close, index=time, columns=code).fillna(method=ffill, limit=10) pre_close = pd.pivot_table(price, values=pre_close, index=time, columns=code).fillna(method=ffill, limit=10) idx = close.index CMRA = {} for i in track(range(len(close)-window+1), description=正在计算CMRA...): close_ = close.iloc[i:i+window, :] pre_close_ = pre_close.iloc[i, :] pre_close_.name = pre_close_.name - pd.Timedelta(days=1) close_ = close_.append(pre_close_).sort_index().iloc[list(range(0, 253, 21)), :] r_tau = close_.pct_change().dropna(how=all) Z_T = np.log(r_tau+1).cumsum(axis=0) CMRA[idx[i+window-1]] = Z_T.max(axis=0) - Z_T.min(axis=0) CMRA = pd.DataFrame(CMRA).T CMRA.index.name = time CMRA = pd.melt(CMRA.reset_index(), id_vars=time, value_name=Cumulative_range).dropna() factor = factor.merge(CMRA) clear_output() return factor.sort_values(by=[time, code]) f = cal_Volatility(count=3) f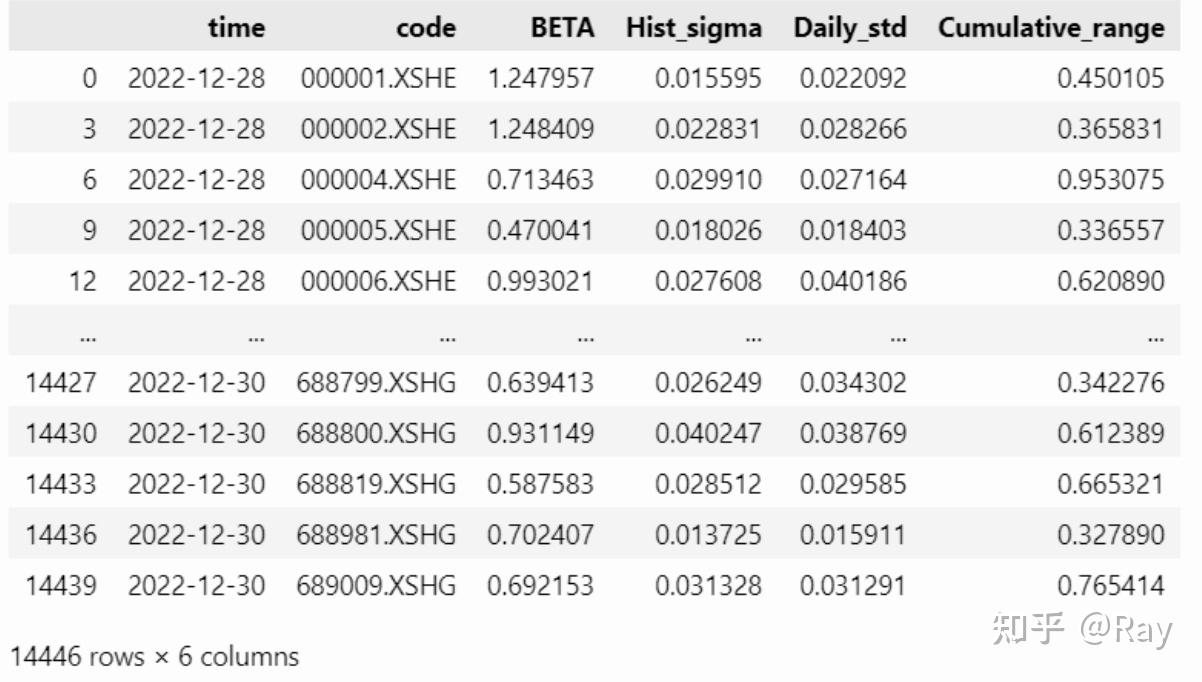
4.活动性（Liquidity）
4.1.因子定义
Liquidity（一级因子） Liquidity（二级因子）
Monthly share turnover（三级因子）：月换手率。对比来21个交易日的股票换手率乞降，然后取对数。\mathrm{STOM}=\ln(\sum_t \mathrm{turnover}_t) \\
Quarterly share turnover（三级因子）：季换手率。计算公式定义如下（T=3）：\mathrm{STOQ}=\ln(\frac{1}{T}\sum_{\tau}^T \exp(\mathrm{STOM}_\tau)) \\
Annual share turnover（三级因子）：年换手率。将上式中的T酿成12。Annualized traded value ratio（三级因子）：年化交易量比率。对日换手率停止加权乞降，时间窗口为252个交易日，半衰期为63个交易日。4.2.代码实现 4.2.1.数据筹办活动性因子计算次要利用了股票的换手率数据，而换手率数据保留在估值数据表格中。我们先利用以下代码提取并整理数据。留意，那里的换手率为百分比形式，我们需要对其停止转换。此外，操纵pandas数据透视表，能够将面板数据转化为矩阵形式。
codes=None start_date=None end_date=None count=250 s, end_date = __start_end_date__(start_date=start_date, end_date=end_date, count=count) start_date, _ = __start_end_date__(start_date=None, end_date=s, count=252) tmp = get_valuation(codes=codes, start_date=start_date, end_date=end_date, count=count, fields=[turnover_ratio]) tmp[turnover_ratio] /= 100. tmp = pd.pivot_table(tmp, index=time, columns=code, values=turnover_ratio)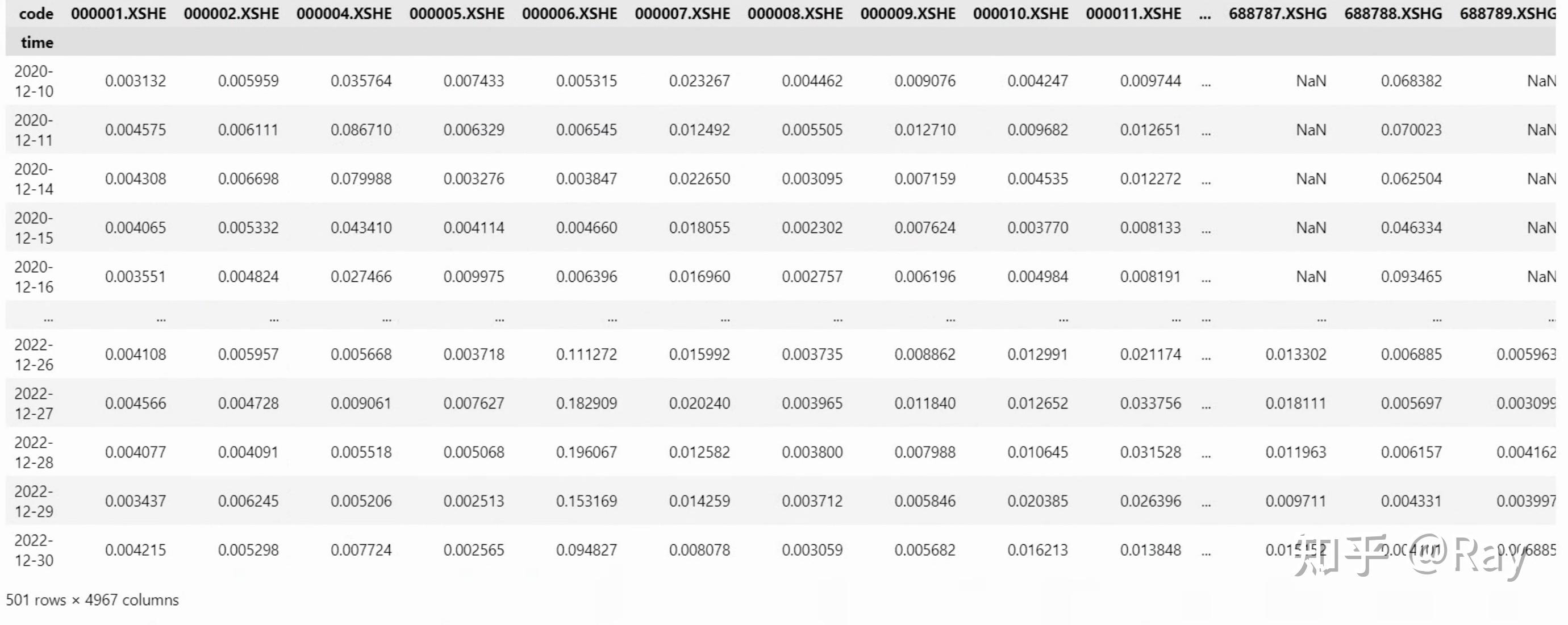
4.2.2.STOM、STOQ和STOA
那些因子计算过程相对简单，纯熟利用pandas索引即可快速计算因子值：
monthly_share_turnover = np.log(tmp.rolling(21).sum()) idx = list(range(20, 252, 21)) quarterly_share_turnover, annual_share_turnover = {}, {} for i in range(len(tmp) - 251): t = tmp.index[i+251] mst = np.exp(monthly_share_turnover.iloc[i:i+252, :].iloc[idx, :]) quarterly_share_turnover[t] = np.log(mst.iloc[-3:, :].mean(axis=0)) annual_share_turnover[t] = np.log(mst.mean(axis=0)) quarterly_share_turnover = pd.DataFrame(quarterly_share_turnover).T annual_share_turnover = pd.DataFrame(annual_share_turnover).T quarterly_share_turnover.index.name = time annual_share_turnover.index.name = time monthly_share_turnover = monthly_share_turnover.loc[s:end_date, :] monthly_share_turnover = pd.melt(monthly_share_turnover.reset_index(), id_vars=time, value_name=Monthly_share_turnover).dropna() quarterly_share_turnover = pd.melt(quarterly_share_turnover.reset_index(), id_vars=time, value_name=Quarterly_share_turnover).dropna() annual_share_turnover = pd.melt(annual_share_turnover.reset_index(), id_vars=time, value_name=Annual_share_turnover).dropna() factor = monthly_share_turnover.merge(quarterly_share_turnover).merge(annual_share_turnover) 4.2.3.年化交易量比率在此因子的计算过程中，考虑到股票停牌的影响，我对计算办法做了些许调整。即先计算换手率的加权均匀，再对均匀日换手率年化处置。
# 年化交易量比率 window, half_life = 252, 63 L, Lambda = 0.5**(1/half_life), 0.5**(1/half_life) W = [] for i in range(window): W.append(Lambda) Lambda *= L W = np.array(W[::-1])/np.mean(W) annualized_traded_value_ratio = [] for i in range(len(tmp)-251): tmp_ = tmp.iloc[i:i+252, :].copy() annualized_traded_value_ratio.append( pd.Series(np.nanmean(tmp_.values*W.reshape(-1, 1), axis=0), index=tmp.columns, name=tmp_.index[-1]) ) annualized_traded_value_ratio = pd.concat(annualized_traded_value_ratio, axis=1).T * window annualized_traded_value_ratio.index.name = time annualized_traded_value_ratio = pd.melt(annualized_traded_value_ratio.reset_index(), id_vars=time, value_name=Annualized_traded_value_ratio).dropna() factor = factor.merge(annualized_traded_value_ratio) 4.2.4.代码整合 def cal_Liquidity(codes=None, start_date=None, end_date=None, count=250): s, end_date = __start_end_date__(start_date=start_date, end_date=end_date, count=count) start_date, _ = __start_end_date__(start_date=None, end_date=s, count=252) tmp = get_valuation(codes=codes, start_date=start_date, end_date=end_date, count=count, fields=[turnover_ratio]) tmp[turnover_ratio] /= 100. tmp = pd.pivot_table(tmp, index=time, columns=code, values=turnover_ratio) # 月、季、年换手率 monthly_share_turnover = np.log(tmp.rolling(21).sum()) idx = list(range(20, 252, 21)) quarterly_share_turnover, annual_share_turnover = {}, {} for i in range(len(tmp) - 251): t = tmp.index[i+251] mst = np.exp(monthly_share_turnover.iloc[i:i+252, :].iloc[idx, :]) quarterly_share_turnover[t] = np.log(mst.iloc[-3:, :].mean(axis=0)) annual_share_turnover[t] = np.log(mst.mean(axis=0)) quarterly_share_turnover = pd.DataFrame(quarterly_share_turnover).T annual_share_turnover = pd.DataFrame(annual_share_turnover).T quarterly_share_turnover.index.name = time annual_share_turnover.index.name = time monthly_share_turnover = monthly_share_turnover.loc[s:end_date, :] monthly_share_turnover = pd.melt(monthly_share_turnover.reset_index(), id_vars=time, value_name=Monthly_share_turnover).dropna() quarterly_share_turnover = pd.melt(quarterly_share_turnover.reset_index(), id_vars=time, value_name=Quarterly_share_turnover).dropna() annual_share_turnover = pd.melt(annual_share_turnover.reset_index(), id_vars=time, value_name=Annual_share_turnover).dropna() factor = monthly_share_turnover.merge(quarterly_share_turnover).merge(annual_share_turnover) # 年化交易量比率 window, half_life = 252, 63 L, Lambda = 0.5**(1/half_life), 0.5**(1/half_life) W = [] for i in range(window): W.append(Lambda) Lambda *= L W = np.array(W[::-1])/np.mean(W) annualized_traded_value_ratio = [] for i in range(len(tmp)-251): tmp_ = tmp.iloc[i:i+252, :].copy() annualized_traded_value_ratio.append( pd.Series(np.nanmean(tmp_.values*W.reshape(-1, 1), axis=0), index=tmp.columns, name=tmp_.index[-1]) ) annualized_traded_value_ratio = pd.concat(annualized_traded_value_ratio, axis=1).T * window annualized_traded_value_ratio.index.name = time annualized_traded_value_ratio = pd.melt(annualized_traded_value_ratio.reset_index(), id_vars=time, value_name=Annualized_traded_value_ratio).dropna() factor = factor.merge(annualized_traded_value_ratio) return factor cal_Liquidity()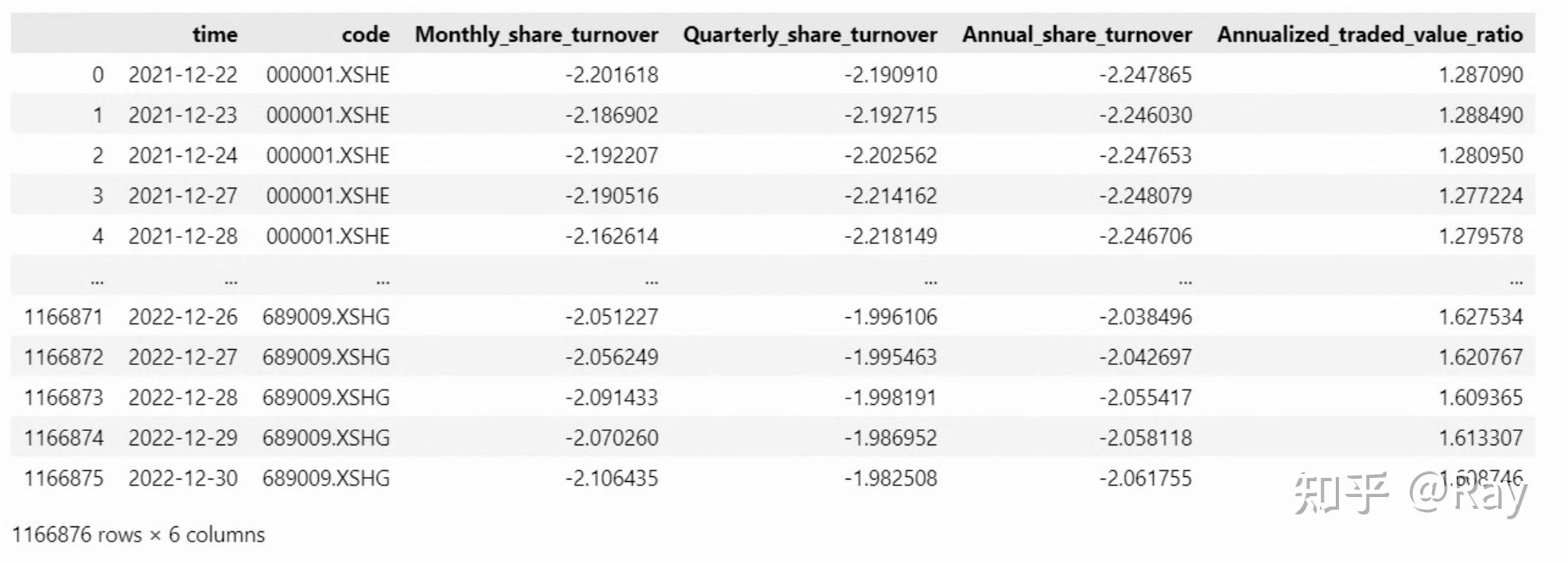
5.动量（Momentum）
未完待续……
0